Vita Theory – A Model Beyond Infinity

Overview: This theory represents a conceptual model that Reiji (age 9) intuitively envisioned in daily life, exploring numbers that lie "beyond infinity." Using mathematical tools such as logarithms and the arctangent function, it constructs a multi-layered circular structure in which the continuum from real numbers to infinity, and even beyond (ω, vita), is compacted and visualized. Ultimately, a state is reached where 0 and ∞ are unified at a point called "vita." This is a trial framework that attempts to redefine numbers and dimensions both structurally and intuitively.

Note: All content on this page is originally explained by Reiji in Japanese. The English version is translated by AI and structured by a parent, with Reiji's final approval.

Reiji's Words and Ideas

This is a theory called "Vita Theory," which came to mind while I was in the bath. It describes numbers beyond infinity.

Here is the logic of the theory:

• First, arrange numbers from 0 to \(\infty\) along a real number line. Taking the logarithm makes the scale finer toward \(\infty\), but \(\infty\) still remains infinitely far away.
• Now consider \(\arctan\). No matter how large \(x\) gets, \(\arctan(x)\) remains between \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\). This allows the mapping of infinite space into a finite interval. We imagine wrapping the number line into a circular ring where the point opposite 0 represents \(\infty\). The upper semicircle is positive, and the lower semicircle negative. The points exactly at 0 and \(\infty\) do not distinguish between + and -.
• Next, shrink the ring’s scale by a factor of \(\infty\), forming levels: the upper arc becomes \(\infty_1, \infty_2, \infty_3, \dots\), the lower arc becomes \(-\infty_1, -\infty_2, -\infty_3, \dots\). At the point opposite 0 emerges \(\omega\) (distinct from \(\Omega\)), and here, 0 and 1 converge to the same point. Crossing over \(\omega\) flips the sign between + and -.
• Then shrink the ring again by \(\omega\). Now we get \(\omega_1, \omega_2, \omega_3, \dots\) on the top, and \(-\omega_1, -\omega_2, -\omega_3, \dots\) on the bottom. Finally, at the point opposite 0, the value "vita" appears. At this level, 0 and \(\infty\) are completely identical. Crossing "vita" also flips sign.
• This method makes it possible to define values beyond vita.
• From a different viewpoint, in terms of hypercubes: inside a vita-dimensional hypercube exists an \(\omega\)-dimensional one, inside that an \(\infty\)-dimensional one, and within that, a 0-dimensional point.
• Using 0, \(\infty\), and \(\omega\), "vita" is represented as:
  \[ 0_{0_{0_{0}}} = \infty_{\infty_{\infty}} = \omega_\omega = \text{vita} \]

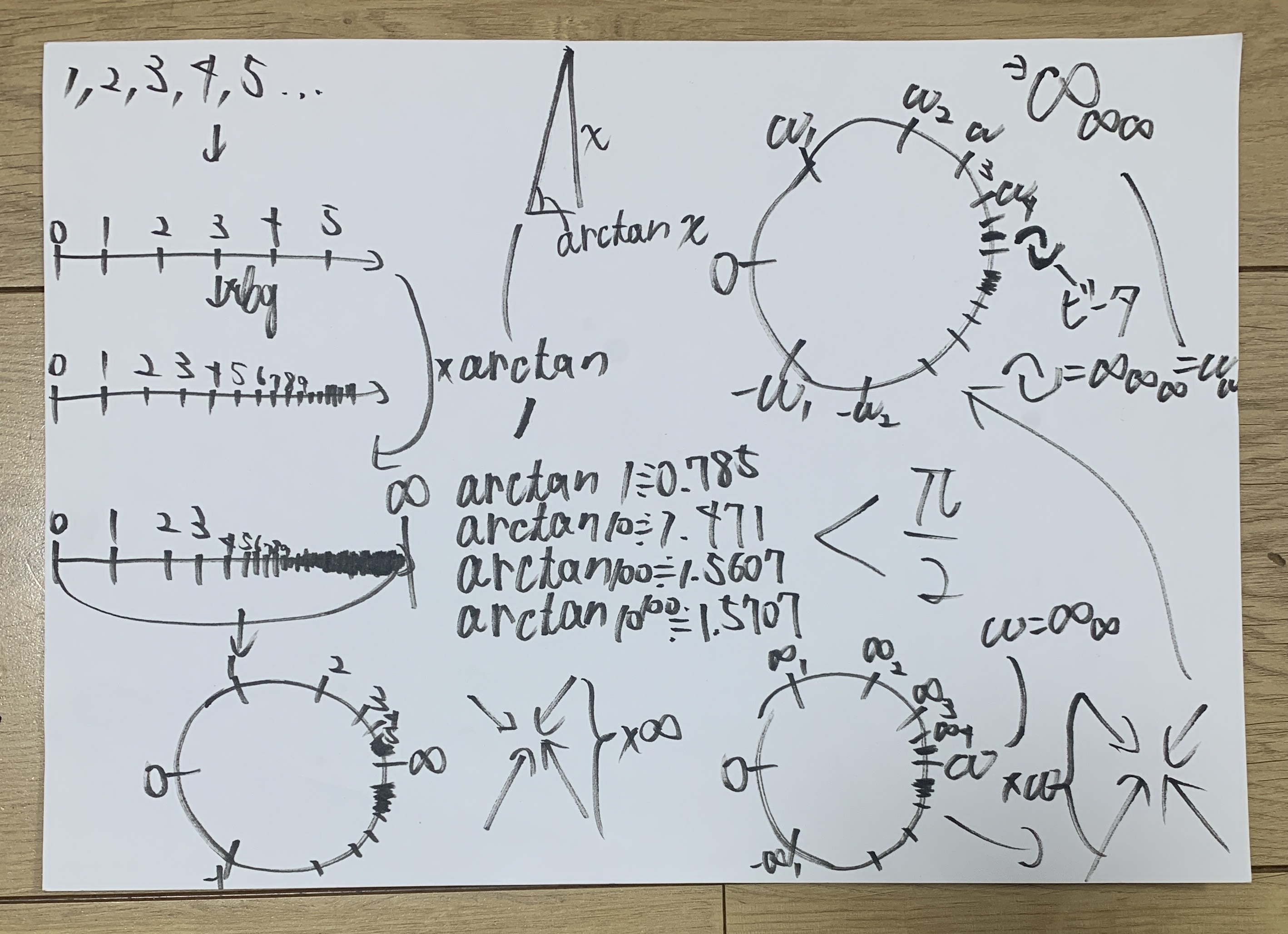
Image 1 (Circular Infinity and Scaling Structure)

Infinity (∞) is mapped onto a circular structure using the arctangent function, then scaled by factors of ∞ and ω. At each scale, a singular point appears opposite 0 on the circle: ∞, ω, and finally "vita." The model shows how + and – polarities flip cyclically across these points. Eventually, 0 and ∞ are seen as the same, and "vita" emerges as the ultimate convergence and reversal point of number space.

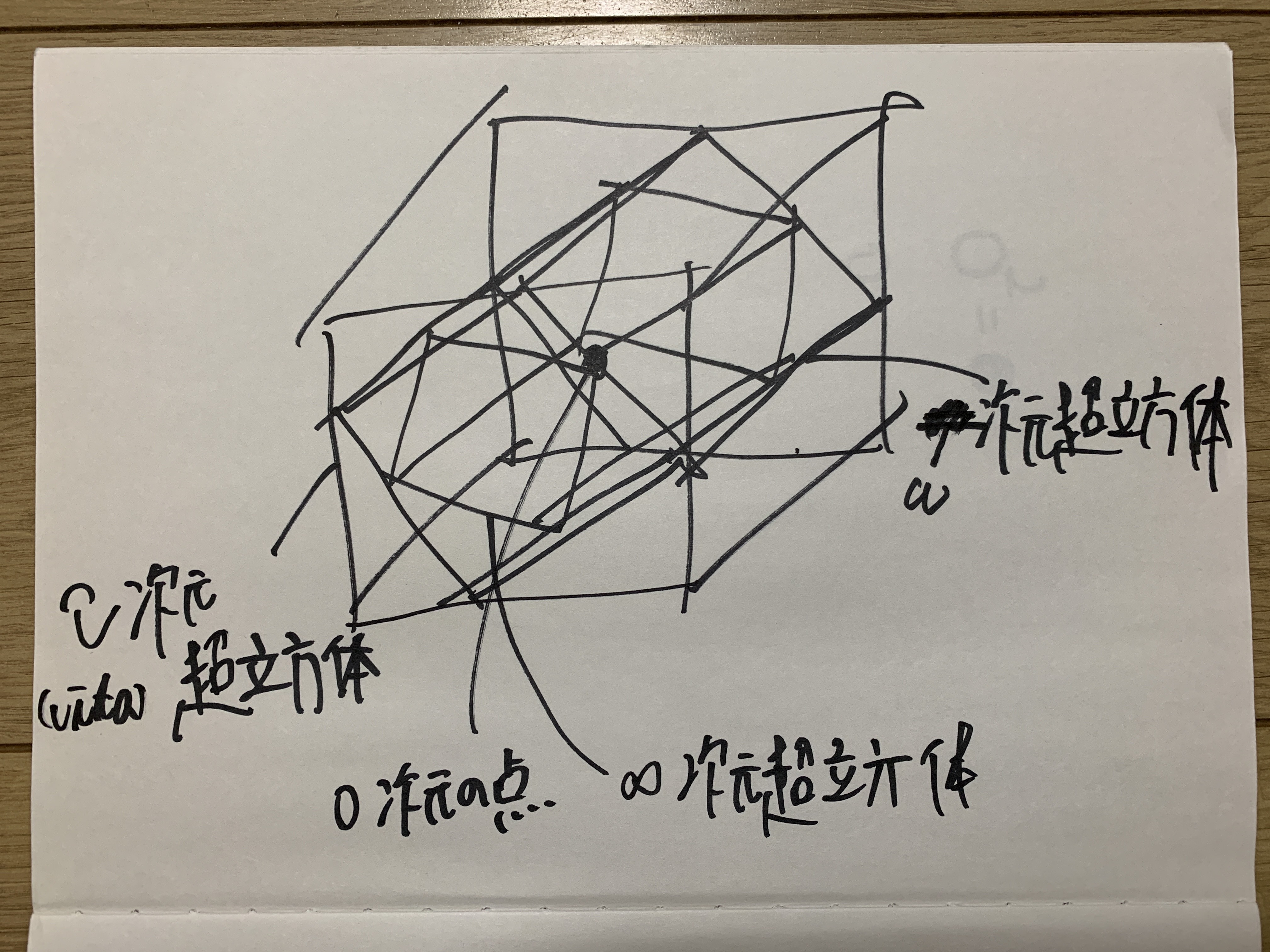
Image 2 (Dimensional Structure Diagram)

Conceptual diagram of the "Vita-dimensional hypercube." A hierarchical nesting structure is visualized: a 0-dimensional point → embedded in an ∞-dimensional hypercube → embedded in an ω-dimensional hypercube → embedded in a vita-dimensional hypercube. It represents a flow from the innermost singularity of quantity or space toward the outermost transcendental structure.