3D Visualization of Julia Set — Dimensional Folding and Structural Analysis

Overview: Inspired by the idea that if the Mandelbrot set can be expressed in 3D, then so can the Julia set, this experiment visualizes the Julia set in three dimensions using Desmos 3D. Normally, complex numbers are represented as \( Z = R + bi \), but Reiji introduced a “folded” model where \( R \) and \( I \) are treated differently to enable three-dimensional representation. By limiting the imaginary component \( I \) to real numbers and treating \( R + I = J \), he effectively folded higher-dimensional quaternionic structures into a form that can be displayed within 3D space. The parameter \( c = q + wi \) is controlled by two sliders in Desmos, dynamically altering the Julia set’s shape. Recursive mapping \( z_{n} = f(z_{n-1}) \) is manually defined and repeated seven times to approximate the fractal’s iterative process, ultimately plotted as \( D(a) \) in three-dimensional space. Observing from the +Z axis, the structure diverges outward; from the −Z axis, it resembles a cauliflower-like surface — a striking analogy connecting mathematical complexity to natural form.

Note: All content on this page is originally explained by Reiji in Japanese. The English version is translated by AI and structured by a parent, with Reiji's final approval.

Reiji's Words and Ideas

• I thought that if the Mandelbrot set can be made 3D, the Julia set can be made 3D as well.
• Normally, complex numbers are expressed as \( Z = R + bi \), but when moving to quaternions, both \( R \) and \( I \) contain complex parts, making it four-dimensional. By restricting \( I \) to real numbers and defining \( R + I = J \), I can fold higher dimensions into a 3D structure.
• The reason I vary only the constant \( c \) on a 2D plane is that if both \( R \) and \( I \) were complex, it would become 4D. Keeping \( c \) two-dimensional makes the visualization possible in 3D space.
• The parameters \( q \) and \( w \) correspond to \( c = q + wi \), and when the sliders move, the shape of the Julia set changes dynamically.
• I defined \( f(z) = (z.x^{2} - z.y^{2}, 2z.xz.y) + c \) and \( D(z) = \sqrt{z.x^{2} + z.y^{2}} \). Since Desmos cannot handle recursive functions directly, I manually applied \( z_n = f(z_{n-1}) \) seven times to build the fractal mapping.
• Finally, I plotted \( D(a) \) in 3D. Looking from the top (+Z direction), it diverges upward; from below (−Z direction), it looks like a cauliflower.

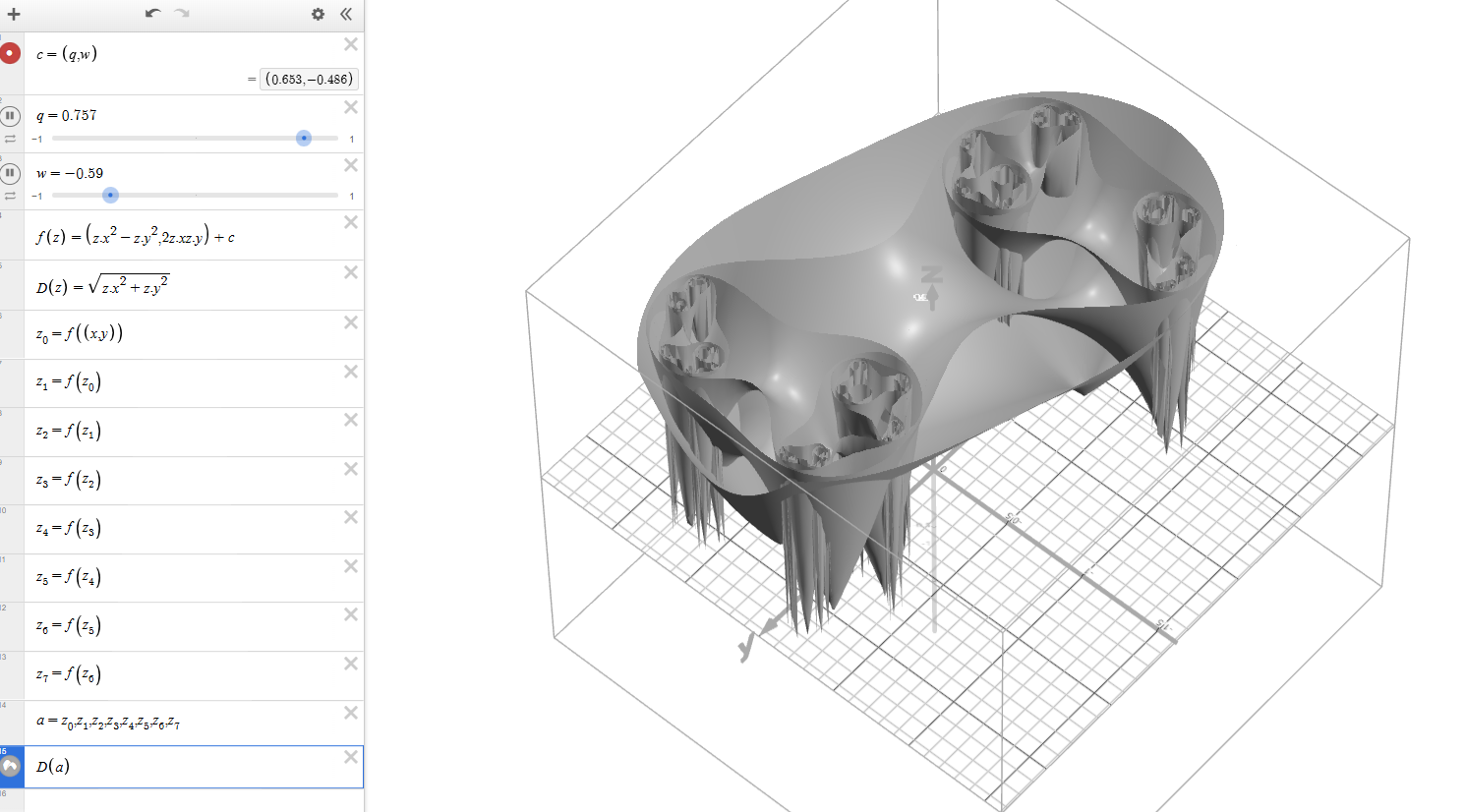
3D Julia Set Visualization (Oblique View)

The recursive mapping \( f(z) = (z.x^{2} - z.y^{2}, 2z.xz.y) + c \) creates a layered self-similar structure, extending in the Z direction with fractal depth.

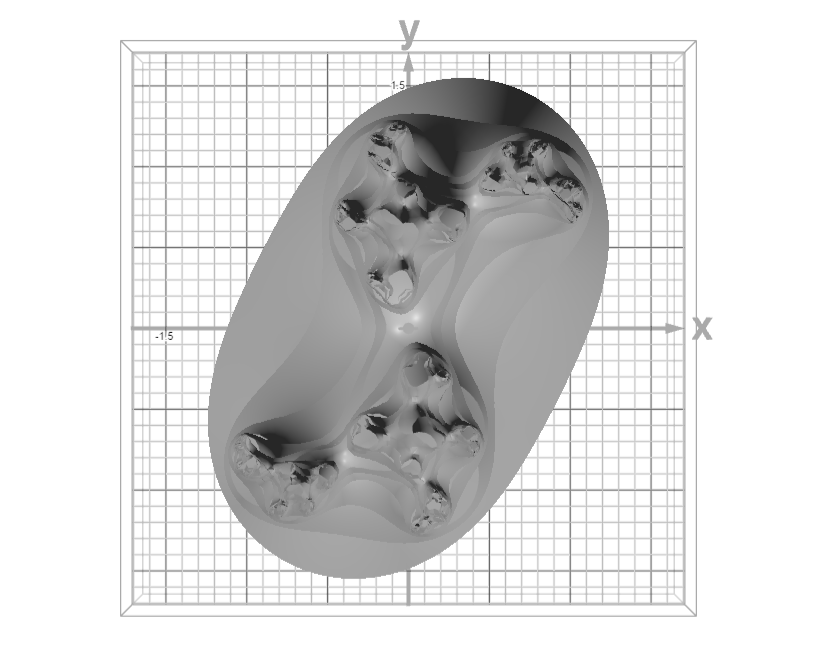
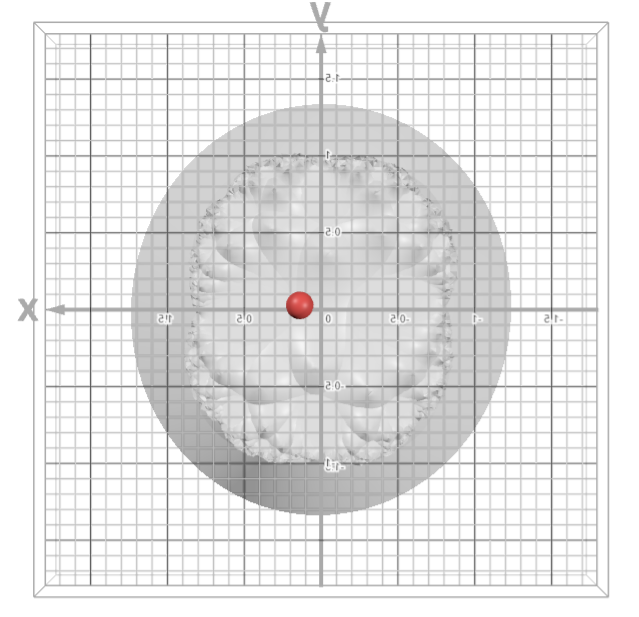
Top View of the Julia Set

A view along the +Z axis showing the complex symmetry and fractal branching. The red point indicates the parameter \( c = q + wi \).

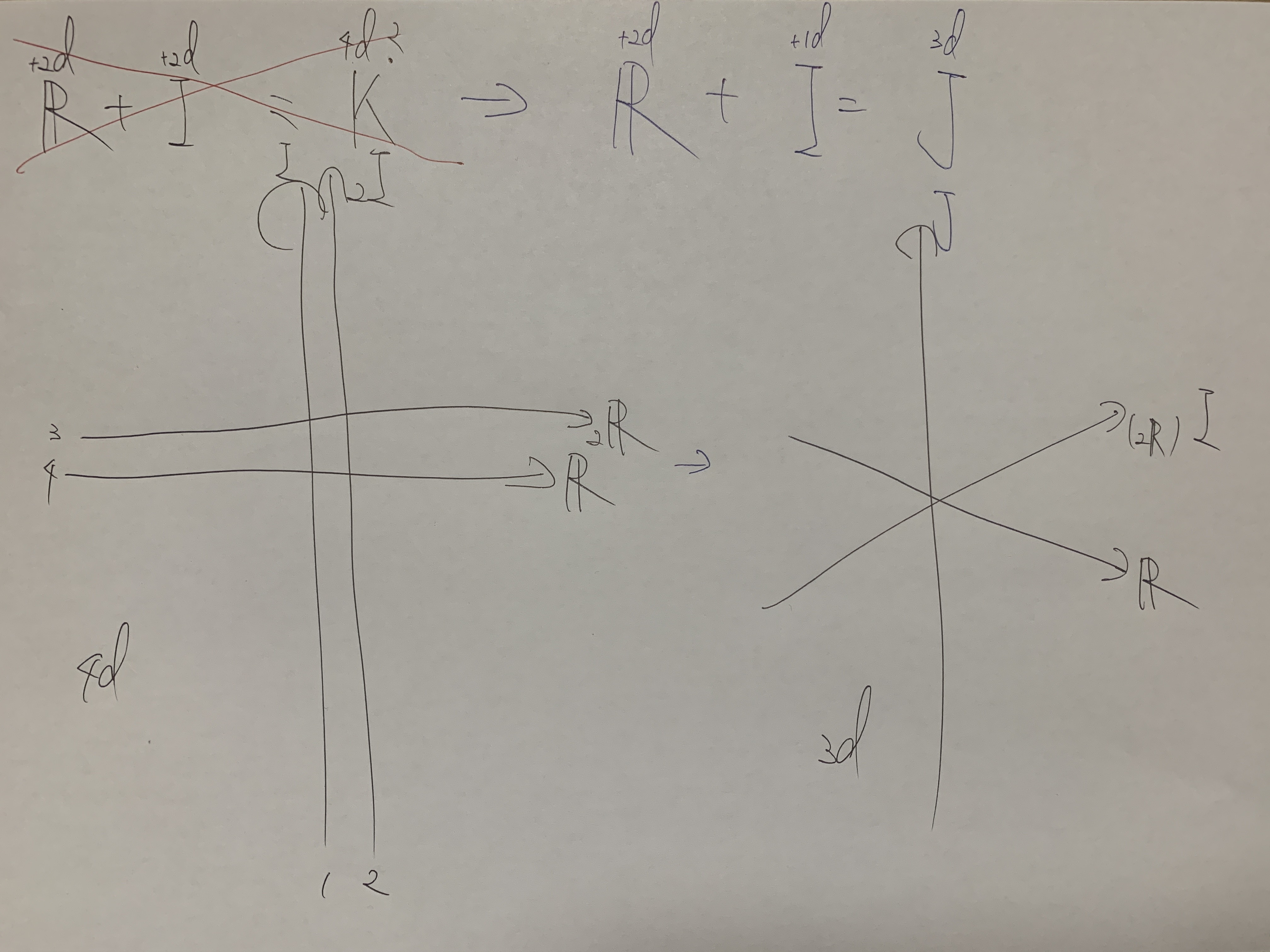
Sketch: Folding Complex and Quaternion Dimensions

A conceptual diagram by Reiji illustrating the process of dimensional folding — from the conventional 2D complex plane (left) to a 3D folded representation (right).

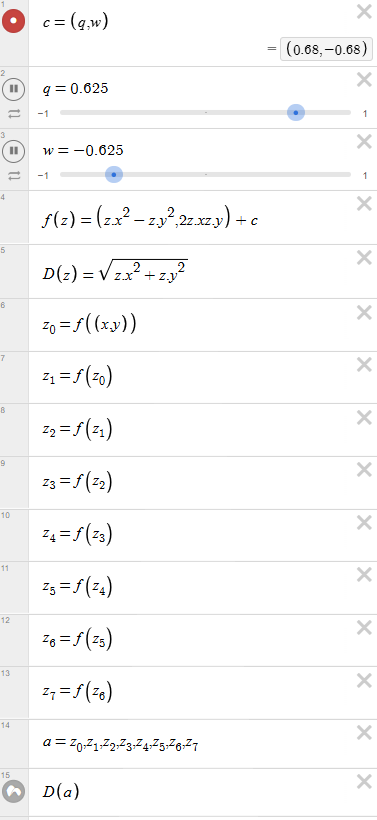
Parameter Example (c = 0.68 – 0.68i)

At this parameter value, the 3D Julia set exhibits multiple symmetry axes and nested self-similar regions reminiscent of natural organic forms.

View from the −Z Axis

From below, the Julia set resembles a cauliflower-like structure — dense, recursive, and richly textured, revealing the internal layers of divergence.