n-EDO Ruler (Equal Temperament Scale Ruler)

This record presents a hand-drawn sketch of a "ruler" that visually aligns various equal divisions of the octave (EDO) on a single line. With 7-EDO at the far left and 5-EDO at the far right, a number of intermediate temperaments such as 12, 19, 31, 53, and 65-EDO are arranged additively.
This layout enables intuitive comparisons of each temperament’s accuracy in approximating just intervals such as pure fifths and thirds. Notably, 53-EDO emerges as a highly precise approximation of both Pythagorean tuning and mean-tone temperament, and the drawing provides visual cues for identifying structural relationships among different EDOs.

Reiji's Observations

• At the left end of the ruler is 7-EDO, and at the right end is 5-EDO. As you move to the right, fourths become narrower and fifths become wider. Moving to the left has the opposite effect.
• New temperaments (EDOs) are added additively—for example, 7 + 5 = 12, 7 + 12 = 19—revealing intermediate EDOs.
• By arranging them visually, it becomes clear how each EDO is structurally related to others.
• The right side of this ruler contains EDOs that approximate the Pythagorean tuning, while the left side contains EDOs that approximate 1/4-comma meantone tuning.
• 53-EDO closely approximates the Pythagorean system and has extremely accurate fifths.
• 53-EDO approximates all intervals within about 7 cents. If you focus on a single interval (e.g., C to E—the just major third is about 386.31 cents, while 31-EDO gives about 387.09 cents, which is very close), then 31-EDO may be more suitable for that specific purpose.
• While the major third in 53-EDO is close to just intonation, the minor third in 19-EDO is more accurate.
• If you reflect this ruler horizontally across the 12-EDO axis (y-axis symmetry), the EDOs on the right often correspond to those on the left with 2 added or subtracted. For example, 43-EDO ⇔ 41-EDO, 55-EDO ⇔ 53-EDO. (This is not always the case, but it often happens.)

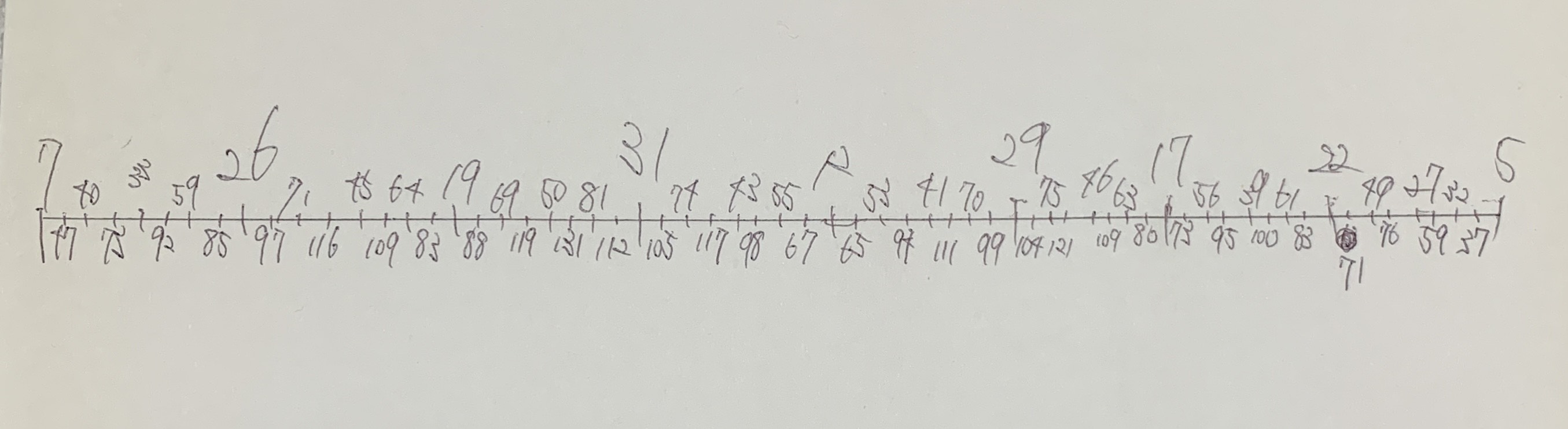
n-EDO Ruler (hand-drawn sketch)

A visual representation of various equal divisions of the octave aligned on a single axis. Midpoints such as 31, 53, and 65-EDO appear between 7 and 5-EDO, allowing intuitive comparison of tuning accuracy for fifths and thirds.