May 6, 2025
Just Intonation Experiment: 28-Tone Design Compatible with 12 Major Keys
This work presents an experimental tuning system based on just intonation, constructed using 28 pitches selected from Euler’s Tonnetz lattice (Euler lattice). The system aims to maintain compatibility with all 12 major chords while limiting the total number of tones to a practical size for standard keyboard instruments.
Unlike equal temperament, which treats commas as equivalent tones, this design preserves the distinct identity of each pitch without tempering commas. As a result, smooth harmonic transitions are achieved while retaining the pure intervals of just intonation. The design prioritizes practical usability by selecting 28 pitches that form structurally clean major triads and allow for modulations under conditional constraints.
This experiment explores a middle ground between harmonic purity and functional versatility, shedding light on how just intonation can be extended to multi-key systems.
Reiji's Observations
- Just intonation is constructed using an Euler lattice, where the +x axis corresponds to 3rd partials, the +y axis to 5th partials, the -x axis to 1/3 partials, and the -y axis to 1/5 partials.
- Equal temperament can be derived by treating commas (interval discrepancies) within the Euler lattice as identical tones.
- This experiment intentionally avoids treating commas as identical tones, and instead fits 28 tones—12 of which form major chords—without resorting to equal temperament.
- To maintain compatibility with current keyboard instruments (like the piano), 28 tones were chosen from just intonation that stack harmonically in thirds or resonate well from reference tones... These 12 tones are tuned so that major chords do not produce beating, while enabling limited modulation.
- A chord with 6/5, 2/3, and 9/5 produces beautiful harmony, but with only the simplest 12-tone selection, the result may include 7/4 instead of 9/5, causing beating.
- Including 9/5 among the 28 tones ensures smoother harmonies.
- The 12 tones corresponding to major chords are: 1/1, 15/16, 9/8, 6/5, 4/5, 4/3, 7/5, 3/2, 8/5, 5/3, 9/5, and 15/8.
- These tones align with pure fifths and major thirds, and the scale allows conditional modulation based on their presence.
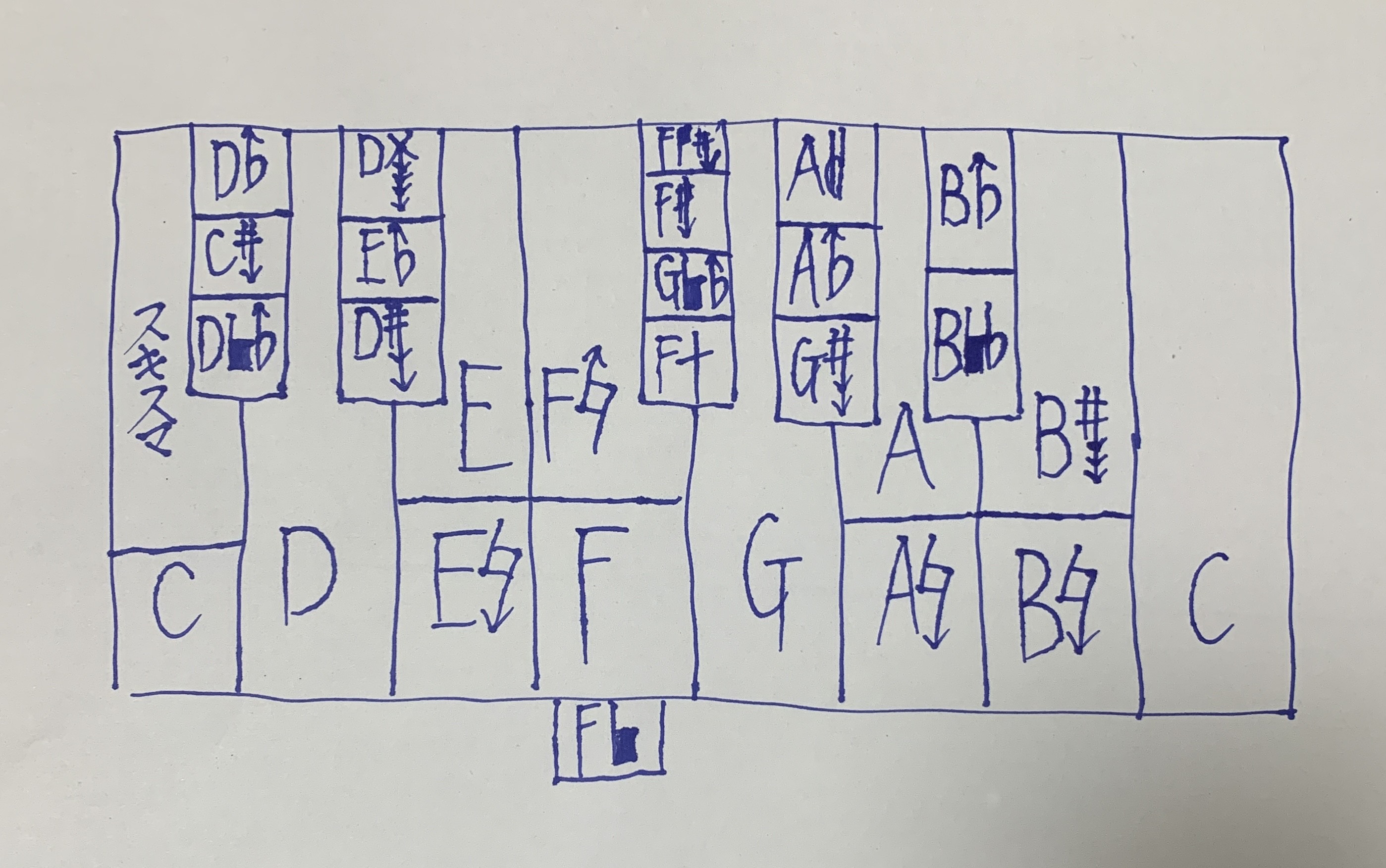
Sketch of the Just Intonation Design
A hand-drawn layout of 28 tones derived from Euler’s lattice. The diagram shows structural relationships used to support major chords in all 12 keys with pure intervals.
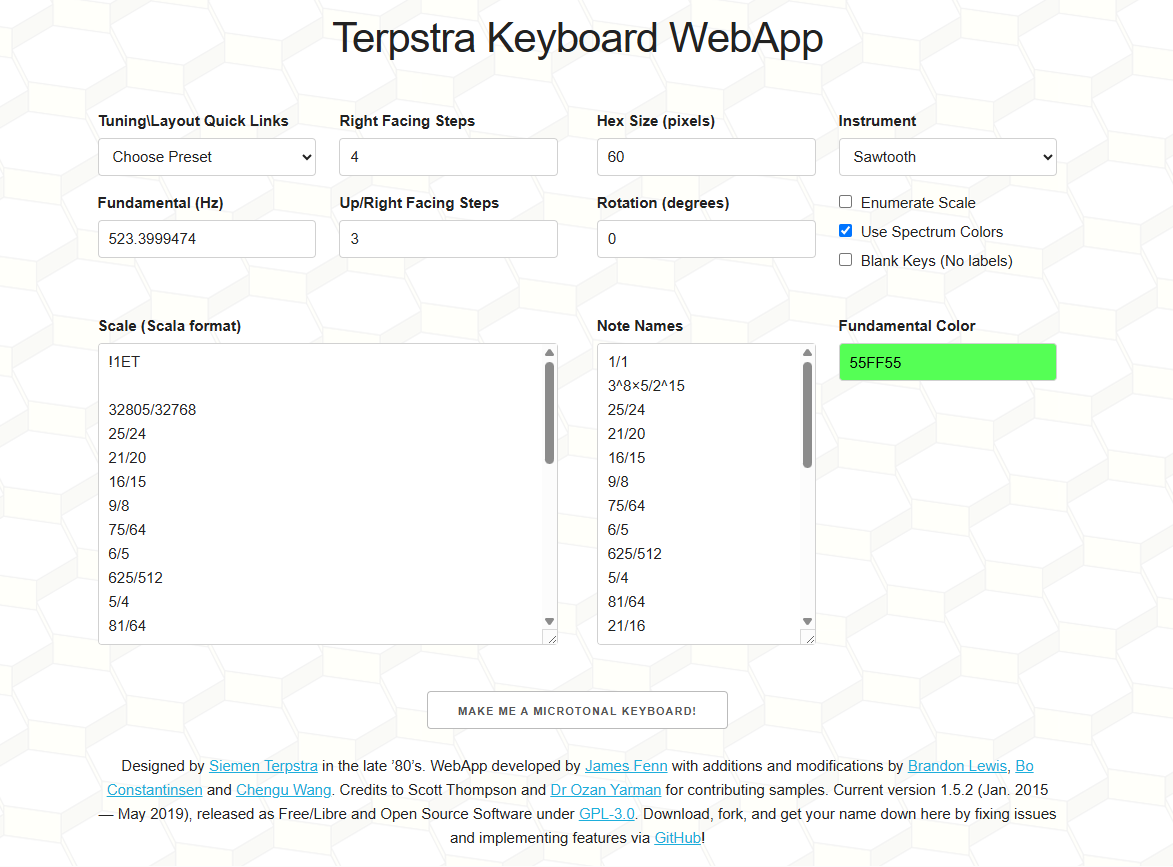
Configuration Screenshot (Terpstra WebApp)
Tuning and color configuration for the 28-tone just intonation system. Frequency ratios are entered in Scala format using rational fractions.
Keyboard Display
Visualization of the 28-tone just intonation layout on the Terpstra Keyboard. Spectrum colors and interval ratios highlight harmonic structures and modulations.
| Output Link | Try it in the Terpstra Keyboard WebApp |
|---|---|
| Tuning Settings |
Fundamental Frequency 523.3999474 Hz Scale (Scala format, in ratios) 32768:32805 / 24:25 / 20:21 / 15:16 / 8:9 / 64:75 / 5:6 / 512:625 / 4:5 / 64:81 / 16:21 / 3:4 / 20:27 / 8:11 / 5:7 / 32:45 / 7:10 / 2:3 / 16:25 / 5:8 / 8:13 / 3:5 / 16:27 / 4:7 / 5:9 / 8:15 / 64:125 / 1:2 |
| Application Used |
Terpstra Keyboard WebApp |
AI Assistant’s Notes and Inferences
- The scale maintains just intonation based on the Euler lattice while ensuring that major chords formed by perfect fifths and major thirds remain pure.
- Modulation is conditionally allowed only through the 12 selected tones, balancing musical theory and instrument practicality.
- Rather than tempering commas, each pitch is preserved independently, maintaining the rigor of just intonation while allowing limited key modulation.
- Including intervals like 6/5, 2/3, and 9/5 enables resonances with the 6th, 9th, and 10th harmonics, resulting in rich overtone alignment.
- With 28 pitches per octave, the design considers the physical constraints of piano keyboards, standing at the intersection of theoretical inquiry and practical implementation.