May 8, 2025
Subdividing the 15/4 Interval: Microtonal Notation and Performance-Tunable Deviations
Overview: This project explores a notational and structural approach to dividing the 15/4 just interval into equal steps of 15, 10, and 5, inspired by Bohlen–Pierce concepts but diverging from it in tuning and application. Each subdivision is notated with microtonal accidentals and includes cent deviation annotations below each note. These annotations serve as performer instructions for interpreting pitches with ±10 cent accuracy.
The design aims to capture the full spectrum between conventional tones, embracing ambiguity and performer agency. It also proposes a flexible tuning strategy that bridges microtonality and perceptual harmony across several expressive resolutions.
Note: All content on this page is originally explained by Reiji in Japanese. The English version is translated by AI and structured by a parent, with Reiji's final approval.
Reiji's Words and Ideas
This is a notated exploration inspired by Bohlen-Pierce, dividing the interval of \(\frac{15}{4}\) from a reference tone into 15, 10, and 5 equal parts from the left.
The number of cents each pitch increases by is calculated as follows:
- \(\sqrt[15]{\frac{15}{4}} \approx 153\text{¢}\)
- \(\sqrt[10]{\frac{15}{4}} \approx 229\text{¢}\)
- \(\sqrt[5]{\frac{15}{4}} \approx 458\text{¢}\)
These resulting tones are notated using microtonal accidentals, approximated within ±10 cents.
Since microtonal symbols are not assigned in 1-cent steps, the cents of deviation are written below each note to allow performers to adjust during interpretation.
Tones enclosed in Gaussian brackets like \(\lfloor \cdot \rfloor\) indicate equivalence—such as treating C and D𝄫 as close enough to be considered the same.
This notation spans from C to B approximately one octave higher, producing a different sonic texture from Bohlen-Pierce.
“Since it’s in the middle of everything, I think it holds a bit of the image of every piece. So I thought it might be good to use when you want to combine all those images into a single piece.”
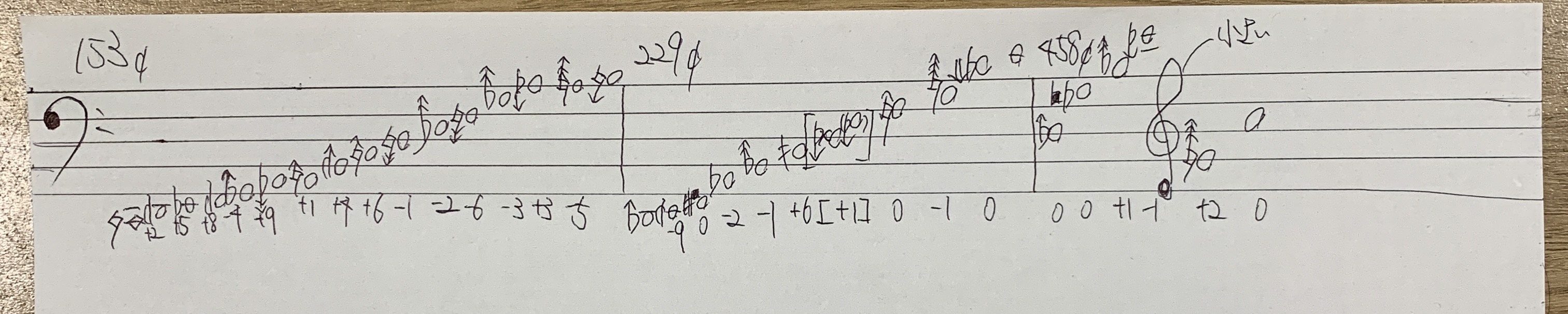
Notated Scale Using Subdivided 15/4
Each pitch step approximates a division of the 15/4 interval (major 13th), subdivided into 15, 10, and 5 equal parts. Microtonal deviations are annotated in cents beneath each note.
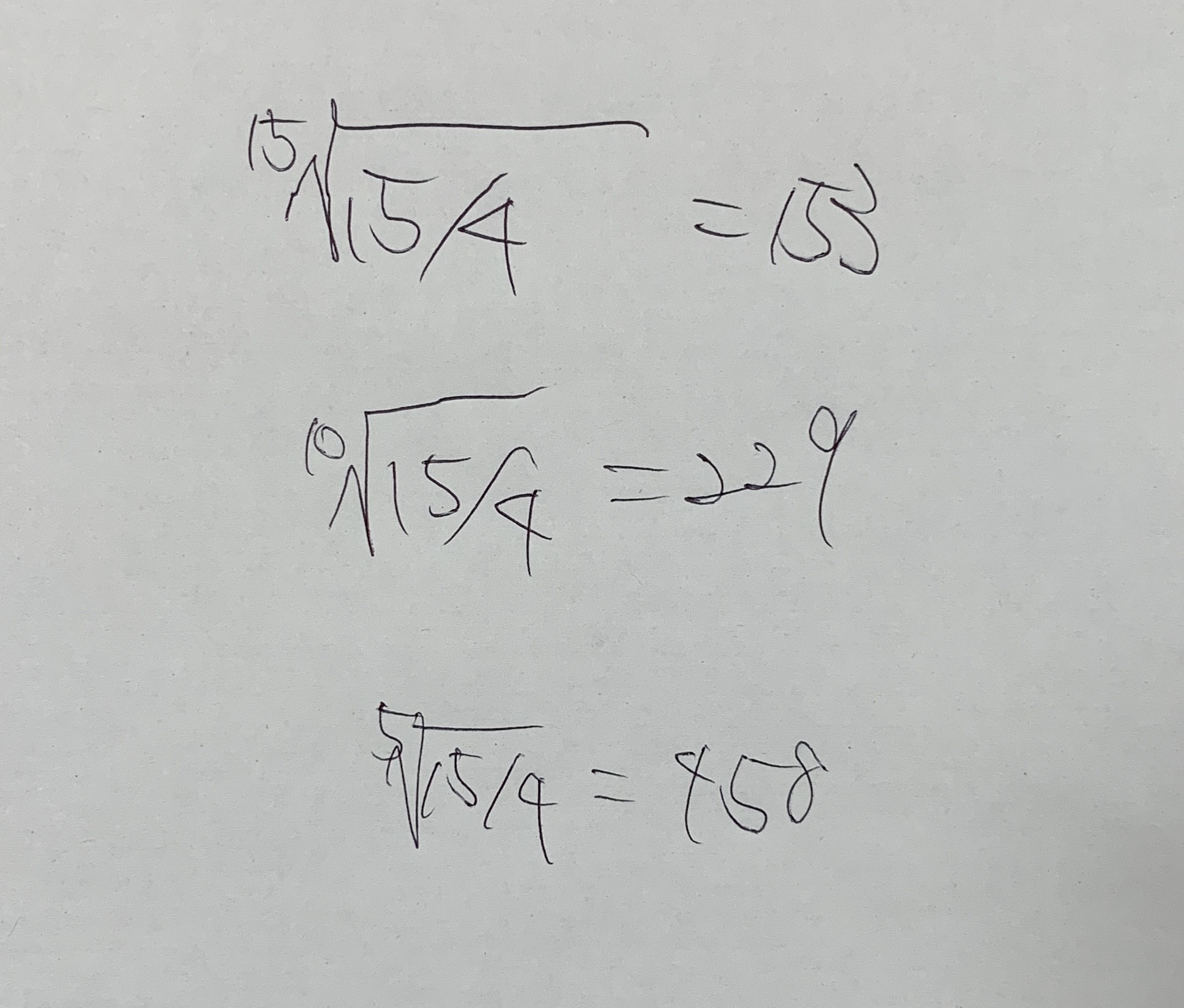
Root-Based Interval Calculations
Square roots and nth roots of the 15/4 interval are calculated to determine equal divisions (e.g., 153¢, 229¢, 458¢), used for tuning microtonal steps in a mathematically consistent way.
| Output Link |
Terpstra Keyboard WebApp Renderings 15 divisions (153¢)10 divisions (229¢) 5 divisions (458¢) |
|---|---|
| Tuning Settings |
15 divisions: - Fundamental: 377.516 Hz - Scala steps (¢): 153.0, 306.0, 459.0, 612.0, 765.0, 918.0, 1071.0, 1224.0, 1377.0, 1530.0, 1683.0, 1836.0, 1989.0, 2142.0, 2295.0 10 divisions: - Fundamental: 1238.7583 Hz - Scala steps (¢): 229.0, 458.0, 687.0, 916.0, 1145.0, 1374.0, 1603.0, 1832.0, 2061.0, 2290.0 5 divisions: - Fundamental: 11738 Hz - Scala steps (¢): 458.0, 916.0, 1374.0, 1832.0, 2290.0 |
| Application Used |
Hand-drawn on paper All ratio calculations done manually Terpstra Keyboard WebApp |
AI Assistant’s Notes and Inferences
- This notation reflects an original approach inspired by Bohlen–Pierce tuning, in which the just 13th (15/4) interval is divided into equal steps by 15, 10, and 5.
- 153 cents (15 divisions): High-resolution steps suitable for melodic detail and microtonal ornamentation.
- 229 cents (10 divisions): Balanced resolution between structure and expressive flexibility.
- 458 cents (5 divisions): Large intervals that can destabilize tonality and provoke bold modulation.
- Importantly, the score not only uses microtonal accidentals but also specifies the cent error below each note, emphasizing an interpretive design: "notation + correction = perceptual phenomenon." This acknowledges both tuning precision and performer agency.
- The use of Gauss symbols (floor notation) to define identical pitches demonstrates an awareness of the fuzzy pitch boundaries often ignored in 12-TET and affirms the importance of microtonal ambiguity.
- The artist's reflection:
“Since it’s in the middle of everything, I think it holds a bit of the image of every piece. So I thought it might be good to use when you want to combine all those images into a single piece.”
...shows an aspiration to unify harmonic worlds through the aesthetics of in-betweenness.