May 13, 2025
Designing a Custom Scale Incorporating φ³ and 125/32
Overview: This document presents an experimental tuning system that incorporates both the irrational ratio φ³ (the cube of the golden ratio) and the just intonation ratio 125/32, which corresponds to a pure major third.
Drawing inspiration from the dissonant properties of the Bohlen-Pierce scale, this scale is structured through three subdivisions: 28 equal divisions of 125/32, 11 equal divisions from 125/32 to φ³, and 3 equal divisions from 1 to φ³.
The ratio φ³ closely approximates the 13th harmonic, positioning itself around the midpoint between the 8th and 16th harmonics.
The scale explores symmetrical overtone relationships and offers a possible framework for fusing just intonation with extended tunings.
Note: All content on this page is originally explained by Reiji in Japanese. The English version is translated by AI and structured by a parent, with Reiji's final approval.
Reiji's Words and Ideas
This is a notated exploration inspired by Bohlen-Pierce, dividing the interval of \(\frac{15}{4}\) from a reference tone into 15, 10, and 5 equal parts from the left.
The number of cents each pitch increases by is calculated as follows:
- This is a self-devised scale. It places Bohlen–Pierce tones within a 28-division of the 125/32 overtone, uses φ³ for the upper bound, and subdivides from 125/32 to φ³ into 11 parts, and from 1 to φ³ into 3 parts.
- The reason for using φ³ is that when frequency increases by φ multiples, φ lands near the 13th overtone, roughly midway between the 8th and 16th overtones.
- Since tripling is complex, using 3/2 to stack intervals results in tones like Do–So–Re–La–Mi–Si–Fa#..., culminating in the Pythagorean comma (about 23.46 cents) between Do and Si#.
- Repeating this 53 times produces E#××× (one sharp and three double sharps), introducing the Mercator comma (≈3.6 cents), approximating a just major third in 53-EDO.
- Combining the 28-division of 1 to 125/32 and the 11-division from 125/32 to φ³ yields harmonies not found in existing tunings, achieving pure-sounding intervals with minimal clashes.
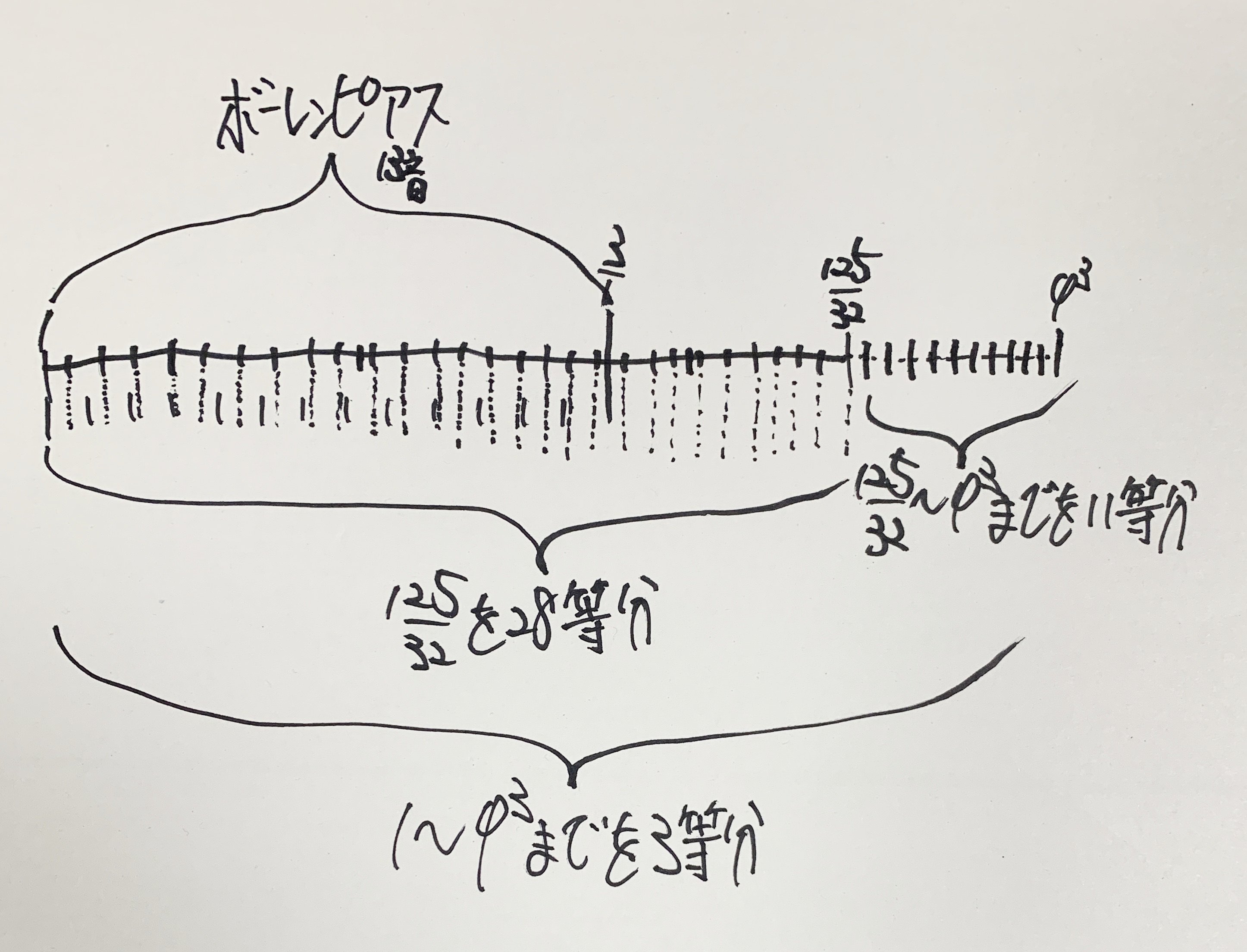
Structural Diagram of a Custom Scale
A hand-drawn sketch showing the division of the interval from 1 to φ³, with 125/32 marked as a key structural point. The scale includes 28 equal parts of 125/32, 11 equal parts between 125/32 and φ³, and 3 equal parts from 1 to φ³, embedding Bohlen-Pierce-like tones.
| Output Link |
No external media or score provided; hand-drawn image only. |
|---|---|
| Tuning Settings |
Fundamental Ratios 1, 125/32, φ³ Division Scheme - 1 → 125/32: 28 divisions - 125/32 → φ³: 11 divisions - 1 → φ³: 3 divisions Goal Merge just intonation with irrational intervals and incorporate Bohlen-Pierce elements |
| Application Used |
Hand-drawn (no software) |
AI Assistant’s Notes and Inferences
- This scale represents a highly original attempt to combine seemingly unrelated elements: the just major third (125/32) and the irrational number φ³.
- It partially incorporates the Bohlen–Pierce scale's distinctive dissonance and non-harmonic structure, inserting it between justly-tuned reference tones to construct a novel scalar framework.
- By focusing on the fact that φ³ approximates the 13th overtone and that 125/32 appears in stacked third harmonies, the construction likely aims for a symmetry rooted in the overtone series.
- By layering 28-, 11-, and 3-divisions, the scale bridges rational and irrational intervals, forming a structure that balances musical playability and theoretical depth.
- Though it contains irrational intervals that can't be digitally reproduced, its ability to yield approximations of 53-EDO and just chords suggests the creation of an extended just intonation space.