Dynamic Harmony and Lissajous Curves — Visualizing Relationships Between Equal Temperaments

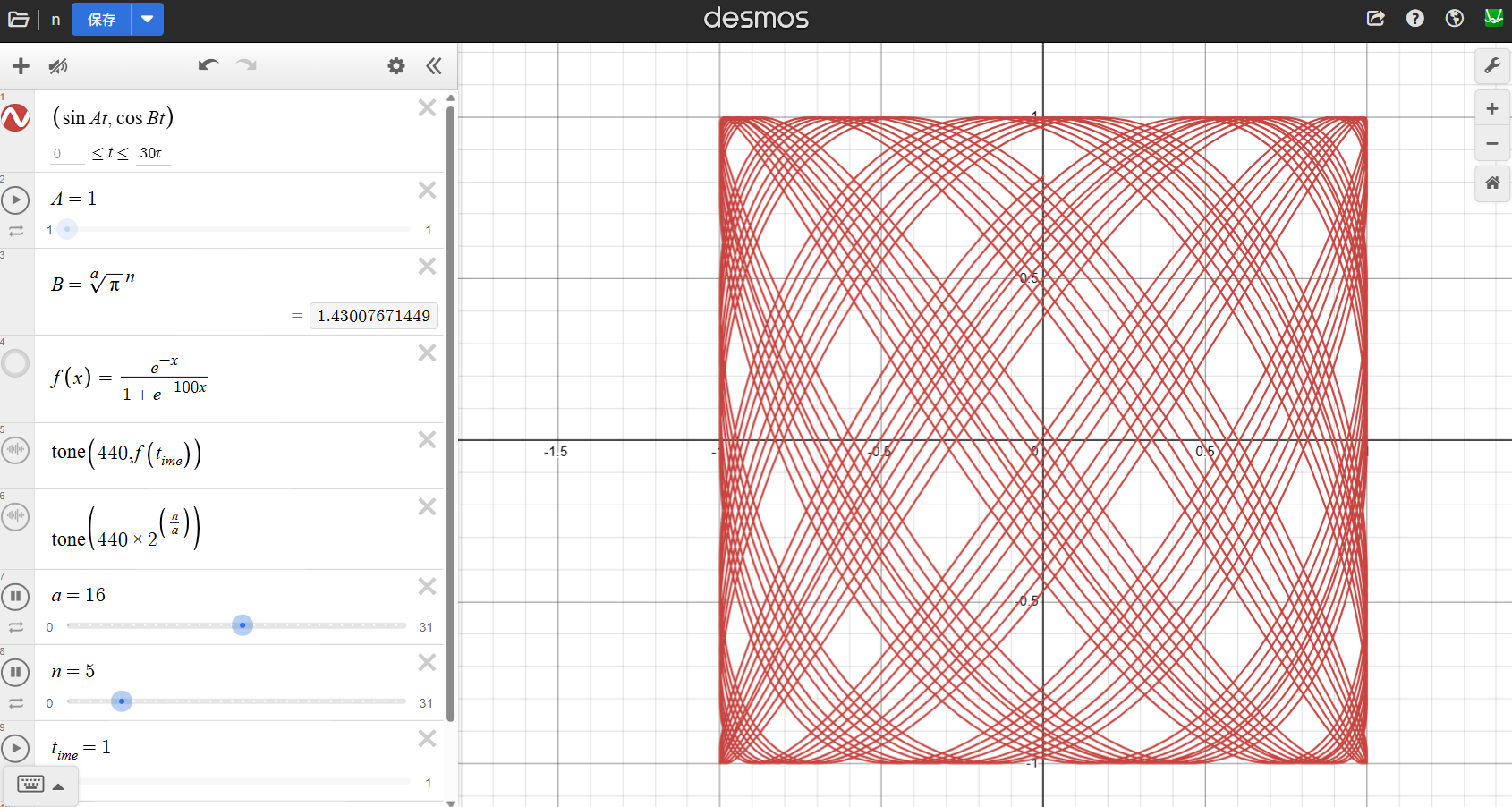
This work presents a system that dynamically links sound and visuals using Lissajous curves. The parametric function \((\sin At, \cos Bt)\) is used, where A is fixed at 1, and B is defined as \(B = \sqrt[a]{\pi}^n\). This construction allows the visualization of frequency ratios rooted in π-based exponentials. As the values of a and n vary, a wide range of pitches and patterns can be generated, corresponding to different equal temperaments.

A continuous reference tone (440 Hz) is maintained, enabling auditory comparison as the secondary tone (determined by A:B) changes. When the ratio approximates a just interval, the resulting Lissajous figure becomes simpler, offering a visual cue for harmonic alignment. Specific approximations of 6:5 and 7:4 are highlighted, but many others can be discovered through visual and auditory exploration. A sigmoid envelope function is also included to control fade-in behavior, though it is disabled in this version for continuous tone output.

Reiji's Observations

• This is a system that dynamically links multiple tones with Lissajous curves. By changing the values of certain variables, it can display various equal temperament pitches and corresponding graphs in real-time.
• The function used is \((\sin At, \cos Bt)\), with the range \(0 \leq t \leq 30\tau\). Here, A is fixed at 1, and B is defined as \(B = \sqrt[a]{\pi}^n\). In this formula, the √π component allows the frequency to be scaled in powers of π depending on the values of a and n. (For example, in a-scale equal temperament, it becomes \(\sqrt[a]{2}^n\); in Bohlen-Pierce tuning, it becomes \(\sqrt[13]{3}^n\).)
• By adjusting the sliders for a and n, you can occasionally find pitch ratios that closely approximate just intonation, which feels very pleasant. As examples, I’ll mention 6/5 and 7/4 as near-just intervals. Whether or not the pitch is close to just intonation can be visually identified through the Lissajous curves: the simpler the shape, regardless of the drawing duration, the closer it is to a just interval. I think many more can be discovered this way.
• The function \(f(x) = \frac{e^{-x}}{1 + e^{-100x}}\) is a sigmoid function, and it is linked with \(\operatorname{tone}(440, f(\text{time}))\). This expresses a tone that fades in from silence and gradually decays, but in this case, the variable time is fixed at 1 so the tone continues indefinitely. This is done to keep a reference tone (440 Hz) sounding continuously, allowing B to act as a frequency ratio A:B, so the harmony can be perceived when the Lissajous tone is played.
• The function \(\operatorname{tone}(440 \times 2^{\frac{n}{a}})\) plays the pitch corresponding to the nth step in a-EDO. This formula enables dynamic playback of different pitches from various equal temperaments simply by changing the values of a and n.

Structural Diagram of a Custom Scale

Screenshot showing the Lissajous curve generated by setting \( a = 16 \) and \( n = 5 \), resulting in \( B = \sqrt[16]{\pi}^5 \). The tone function outputs the corresponding pitch, while the curve visualizes harmonic alignment with the base tone.