Pure Just Tuning — Complete Harmonic Modulation with 8 Notes

Overview: This is a tuning system designed using pure just intervals that form a fully harmonically aligned structure across 8 tones, or 9 if including the octave. Each note is tuned to a rational ratio, allowing perfect harmony within chords and enabling modulation without encountering the wolf intervals typically found in traditional just intonation. The tuning is expressed in a logarithmic framework, enabling symmetry and interchange between perfect fifths and perfect fourths.

Definitions used in this article: “Full harmony” means that, in any key, the selected triad type (e.g., \(4:5:6\), \(9:11:13\), 7-based, etc.) is built entirely from rational (small-integer) ratios. “Wolf-free” means that, within each selected chord, no approximation or breakdown of \( \tfrac{3}{2} \) is required during modulation. This work is not equal temperament; it is a 13-limit just-intonation design.

Examples: C uses \(\{1/1, \, 5/4, \, 3/2\}\) (i.e., \(4:5:6\)). D uses \(\{9/8, \, 11/8, \, 13/8\}\) (i.e., \(9:11:13\), a neutral triad), not a “major” triad.

Fifths–Fourths relation: \(C:C' = 1:2, \; G = \tfrac{3}{2}, \; F = \tfrac{4}{3}\). In cents: \(701.96 + 498.04 = 1200\).
Note that stacking fifths does not literally transform into fourths. Rather, they are complementary in logarithmic space. By switching triad types key by key, this system preserves pure harmony throughout modulation.

Note: All content on this page is originally explained by Reiji in Japanese. The English version is translated by AI and structured by a parent, with Reiji's final approval.

Reiji's Words and Ideas

• This system consists of 8 fully harmonically aligned notes (9 including the octave):
  1/1 , 9/8 , 5/4 , 11/8 , 3/2 , 13/8 , 7/4 , 15/8 , 2/1.
• For example, the C major chord uses \(1/1, 5/4, 3/2\); the D major chord uses \(9/8, 11/8, 13/8\) — all chords are fully harmonious within this system.
• In traditional just intonation, modulation to D from C causes wolf intervals between D and A. This system avoids such breakdowns, achieving full harmonic modulation.
• While stacking perfect fifths typically continues indefinitely, this system — based on logarithmic representation — ensures that \(C:C' = 1:2\), and \(G = 1.5\). As perfect fifths stack, they transform into perfect fourths, and vice versa. This oscillation is key to enabling both harmonic integrity and modulation.
• This duality between perfect fifths and fourths is leveraged to achieve a fully harmonious and modulatable tuning structure.

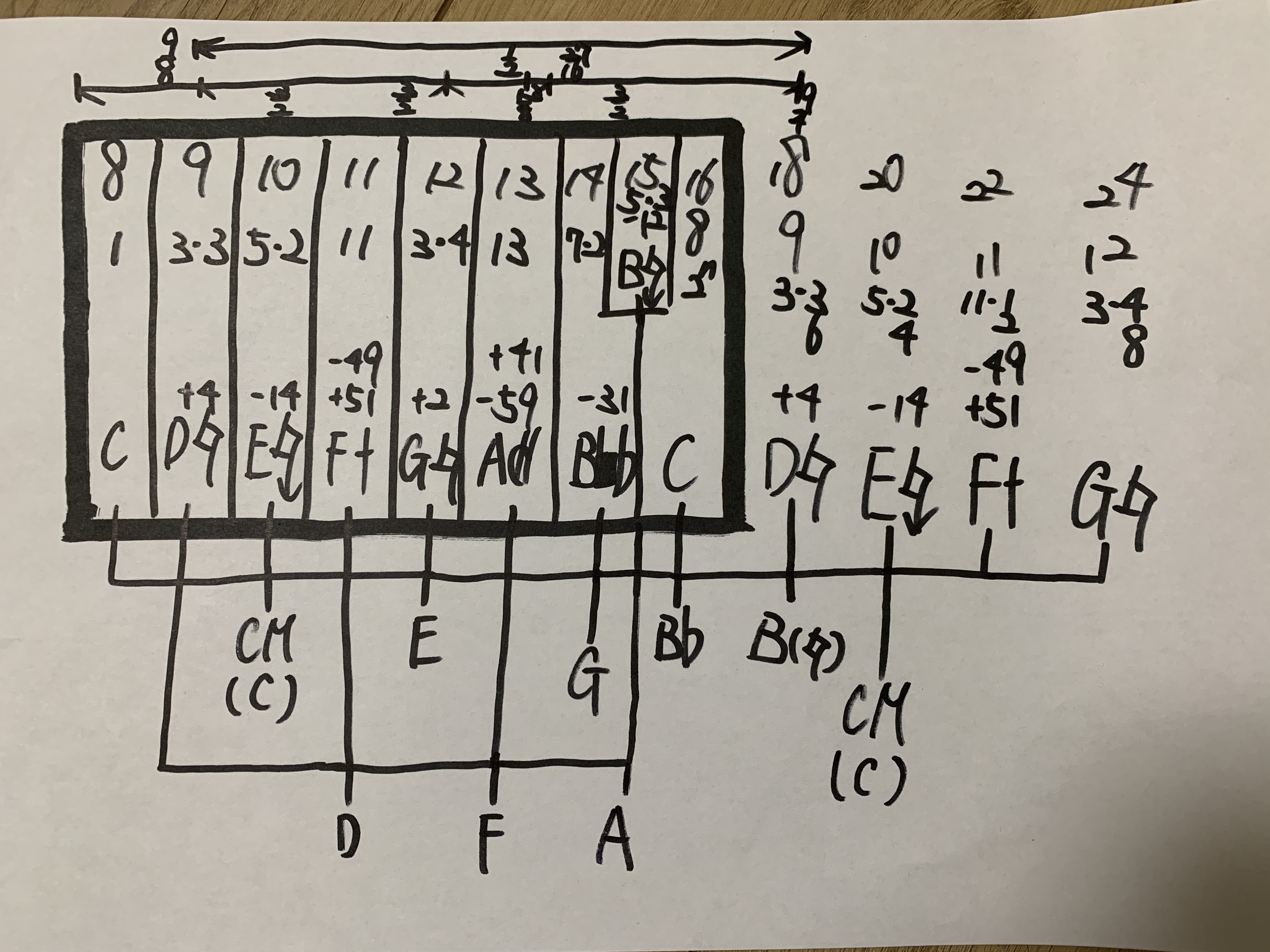
Reiji's Handwritten Diagram

A detailed breakdown of how notes align and modulate across keys, using rational ratios and cent deviations. This sketch reflects the internal logic of Reiji’s system.

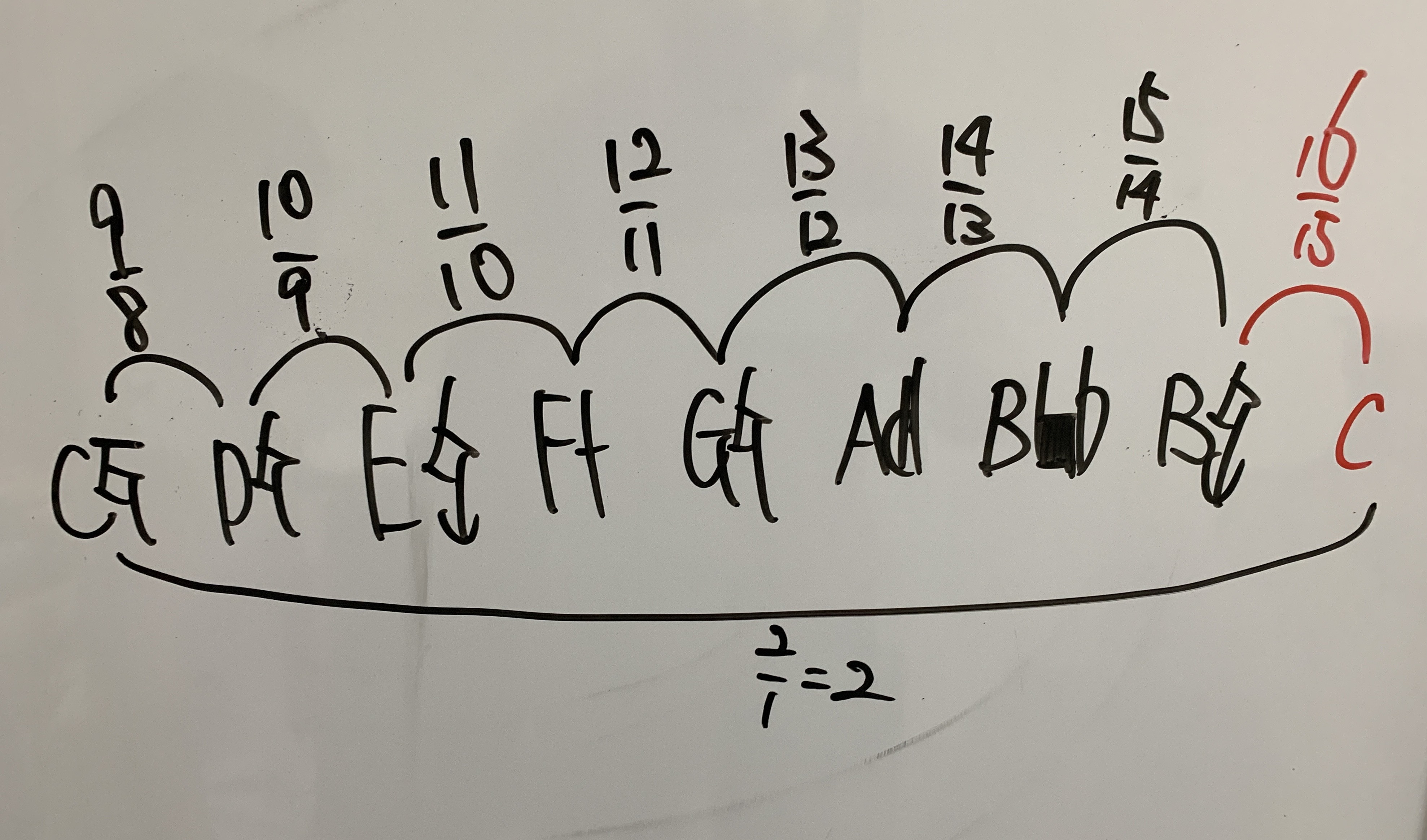
Handwritten Diagram of Second Intervals

A hand-drawn classification of second intervals (minor, neutral, major) in the pure just tuning system, annotated with frequency ratios and approximate cent values. It visualizes the nuanced gradations and the system’s expanded consonant set.

Handwritten Interval Map with Harmonic Ratios

A whiteboard sketch mapping each pitch in the pure just tuning system with its corresponding frequency ratio. It visually traces the sequential relationships between notes, showing how harmonic steps build toward the octave.

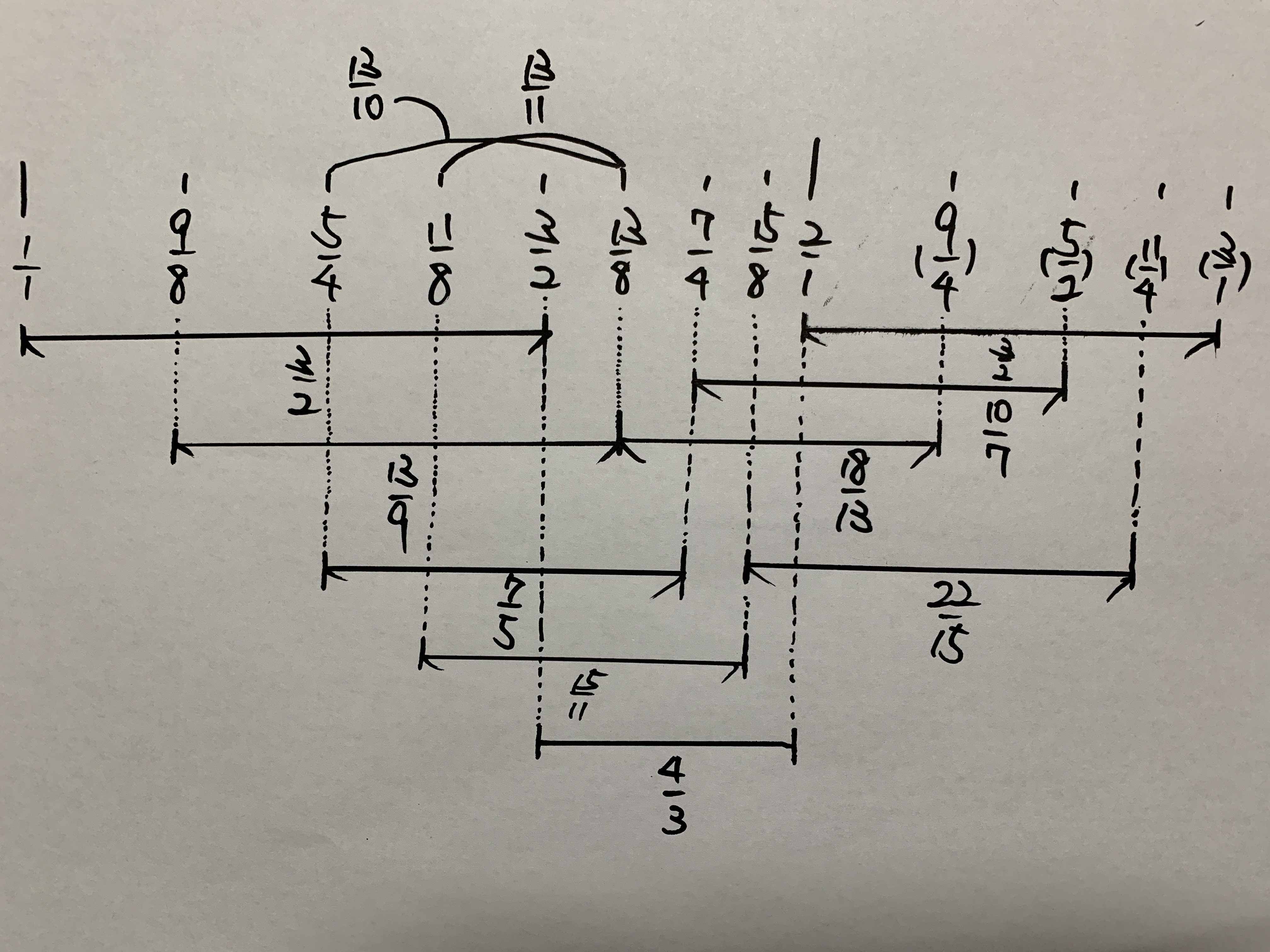
Handwritten structural diagram of pure just tuning

This sketch illustrates the relational logic of the tuning system, showing how each pitch ratio (e.g., 1/1,9/8,5/4,11/8,3/2,7/4) is derived and interconnected. Additional annotations (e.g., 13/9,18/13,22/15) indicate the internal proportional links among intervals.

Factorized Mathematical Representation of Tuning Ratios

A handwritten table listing each note in the pure just tuning alongside its frequency ratio in multiple forms, including prime factorization. This breakdown highlights the structural logic of the system from both musical and mathematical perspectives.

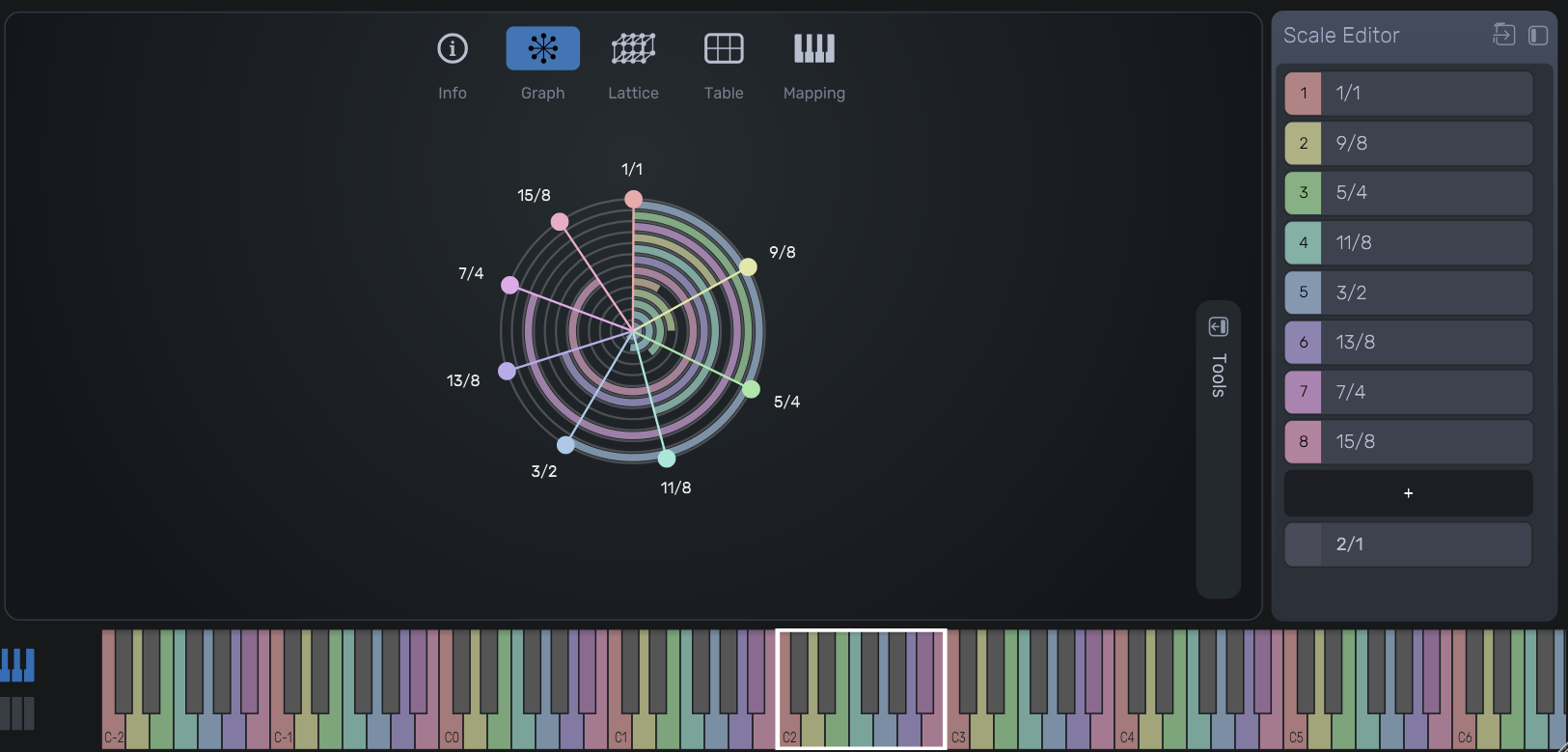
Graph View of Tuning Structure

Graphical representation of the tuning system, showing the harmonic spacing of each tone. Tools such as Entonal Studio were used to model the tuning visually and audibly.

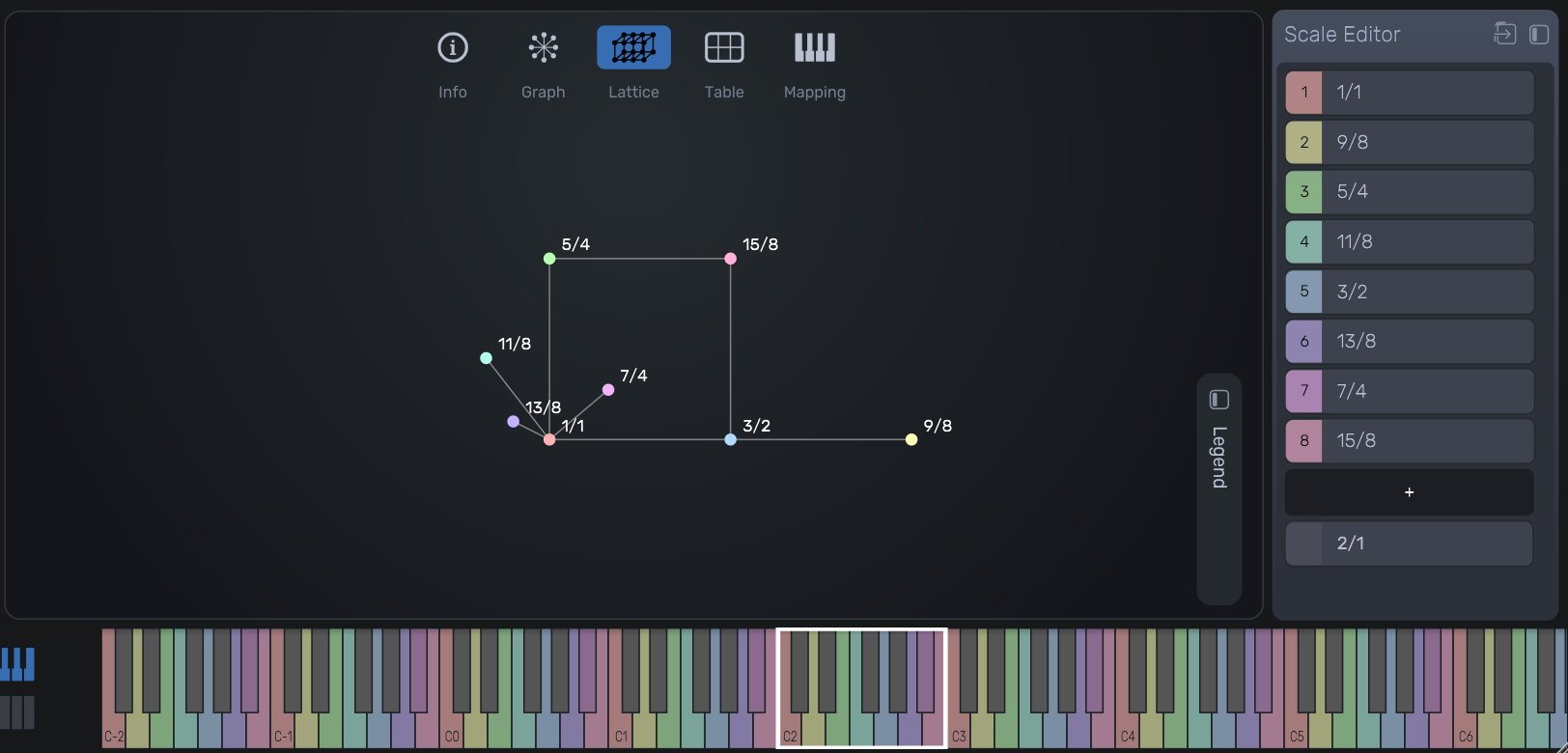
Lattice Diagram of Interval Relations

Lattice view showing intervallic relationships, emphasizing the symmetry and harmonic proximity among all included tones.

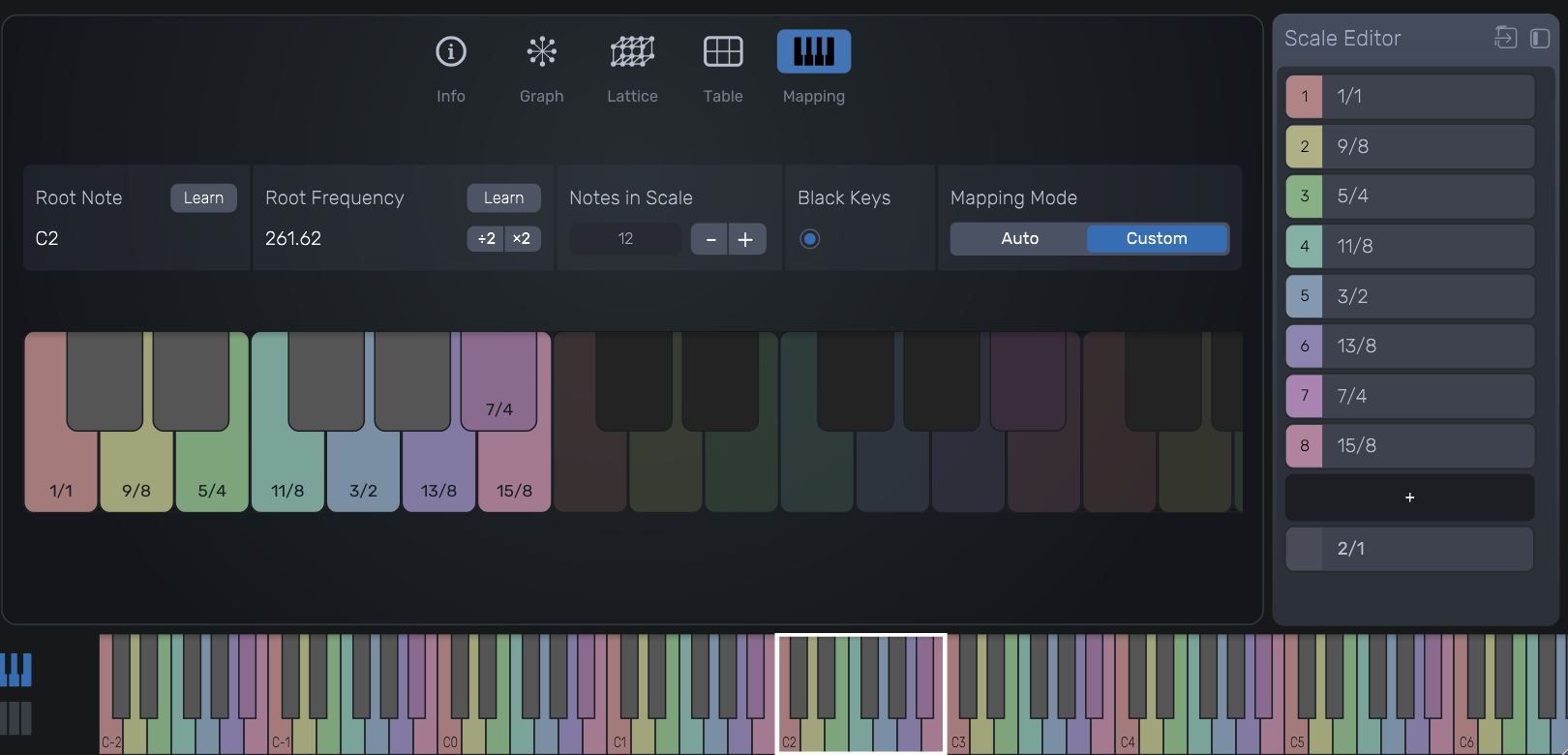
Keyboard Mapping with Ratio Labels

The mapping of just intervals onto a colored keyboard layout, aiding in visual recognition and real-time interaction with the tuning system.