53-EDO Decay Function and Lissajous Visualization — Harmonic Interaction and Temporal Damping

Overview: This Desmos-based project reproduces 53-tone equal temperament (53-EDO) using a piano-like timbre, where each harmonic’s decay is modeled mathematically through a sigmoid envelope. By linking this decay behavior with Lissajous curves, Reiji visualizes overtone interactions and subtle intonational deviations between near-pure harmonic ratios. The experiment demonstrates how time-dependent damping and harmonic amplitude balance can generate visually coherent patterns that correspond to the perception of pitch and tone color.

Note: All content on this page is originally explained by Reiji in Japanese. The English version is translated by AI and structured by a parent, with Reiji's final approval.

Reiji's Words and Ideas

• This experiment reproduces 53-EDO sounds in Desmos with a piano-like tone and visualizes the resulting overtones using Lissajous curves.
• The variable \( t_{ime} \) represents time. When \( t_{ime} \leq 0 \), the sound is silent; when \( 0 \leq t_{ime} \leq 1.5 \), a sigmoid function controls the amplitude, first rising to 1, then gradually decaying.
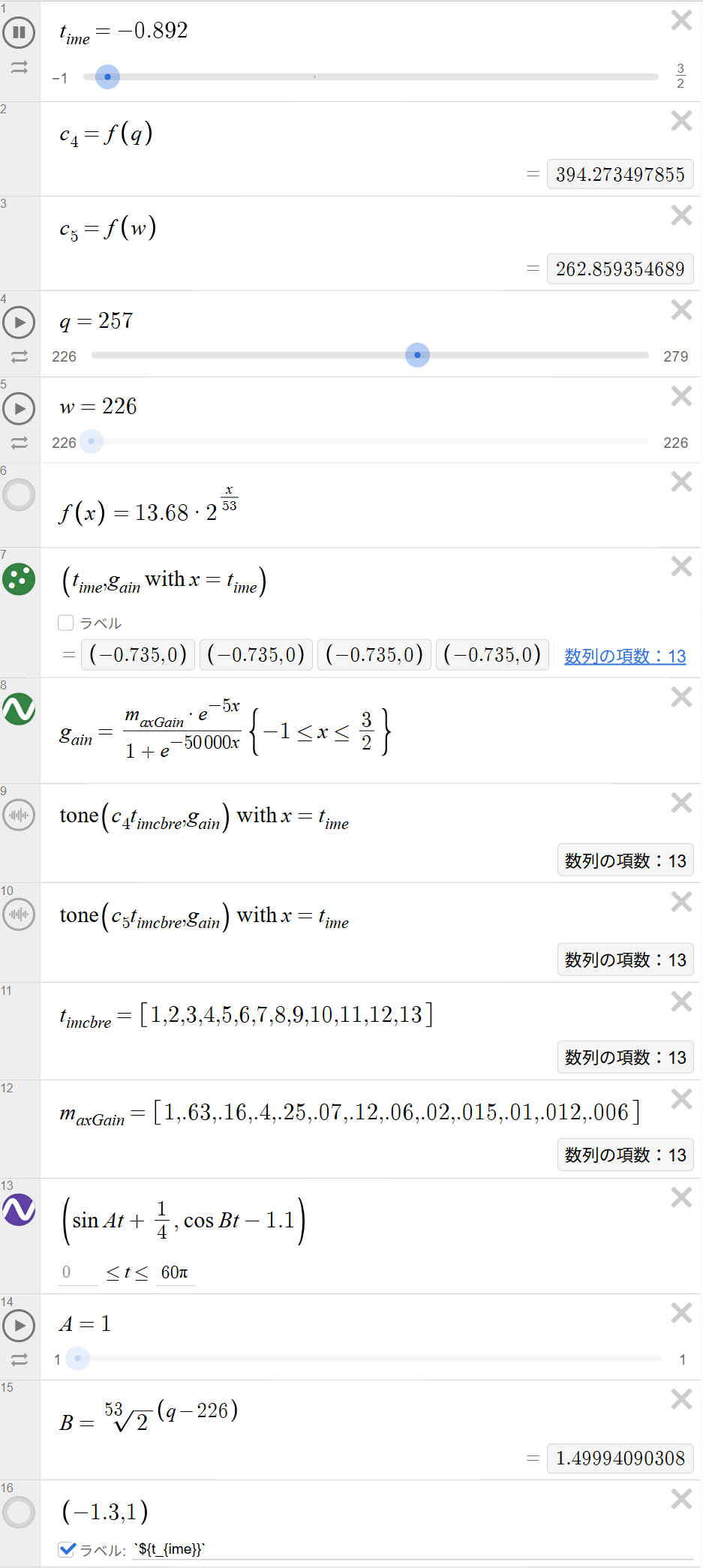
• The expression \( \operatorname{tone}(c_4 t_{imcbre}, g_{ain}) \text{ with } x = t_{ime} \) combines harmonic oscillations and a damping gain function. Up to the 13th overtone is defined, and each amplitude is individually weighted via the array \( maxGain \), imitating the energy distribution of piano overtones.
• By adjusting the variable \( q \), each step of the 53-tone scale produces a slightly different pitch. The parameter \( w \) represents the lower tone, but remains fixed because its alteration results in equivalent frequencies.
• The variables \( q \) and \( w \) correspond to the parameters \( A \) and \( B \) in the Lissajous function. \( A \) is fixed at 1, while \( B \) varies according to \( q \), causing the Lissajous shape to change synchronously with pitch variation.
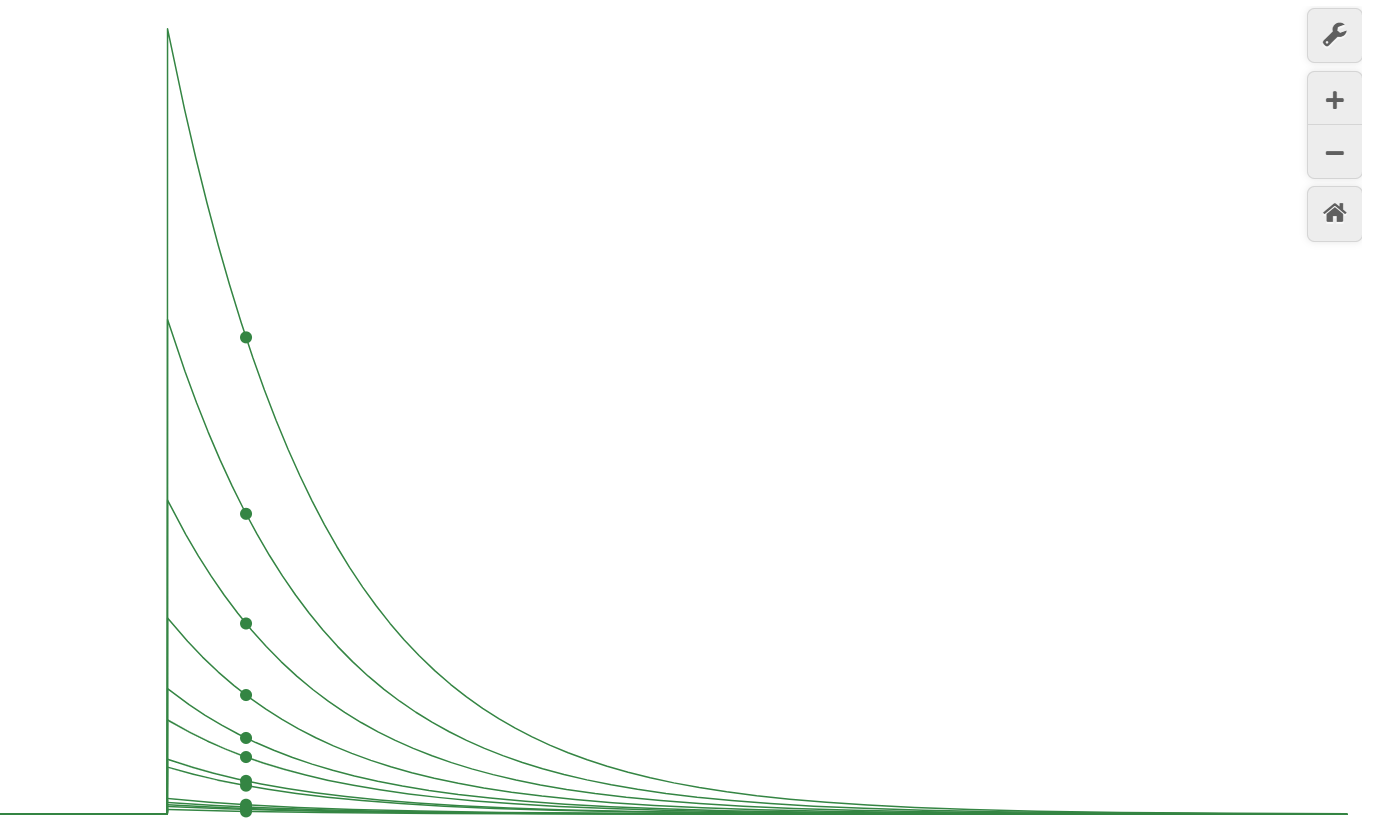
• The sigmoid decay graph allows simultaneous observation of fundamental and overtone attenuation during sound playback.
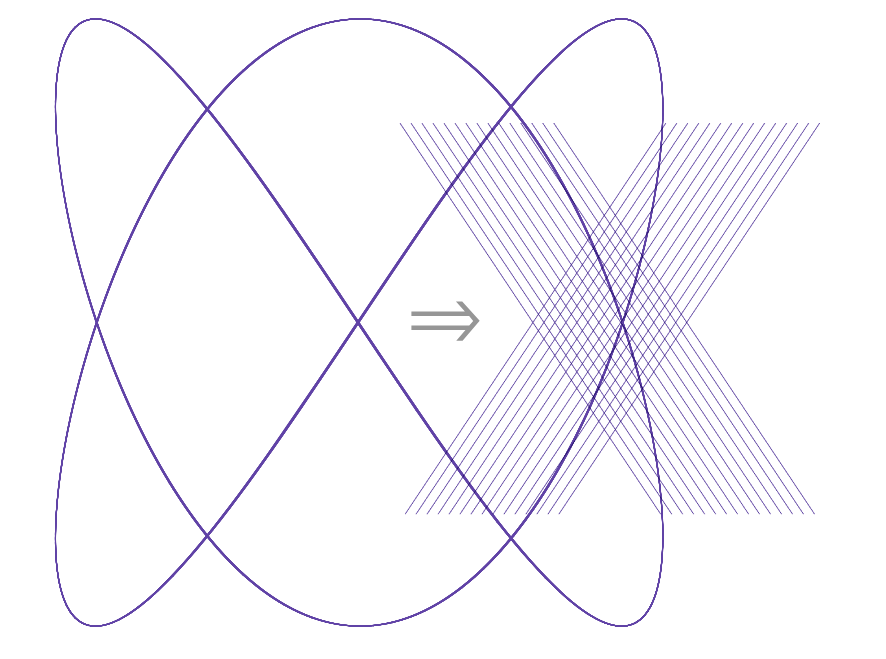
• The Lissajous visualization shows how the periodic alignment between overtones shifts across microtonal steps of 53-EDO. For instance, when \( q = 257 \), the pitch differs from the pure 3:2 ratio by only 0.07 cents—an almost imperceptible difference—yet the line intersections subtly diverge upon magnification.

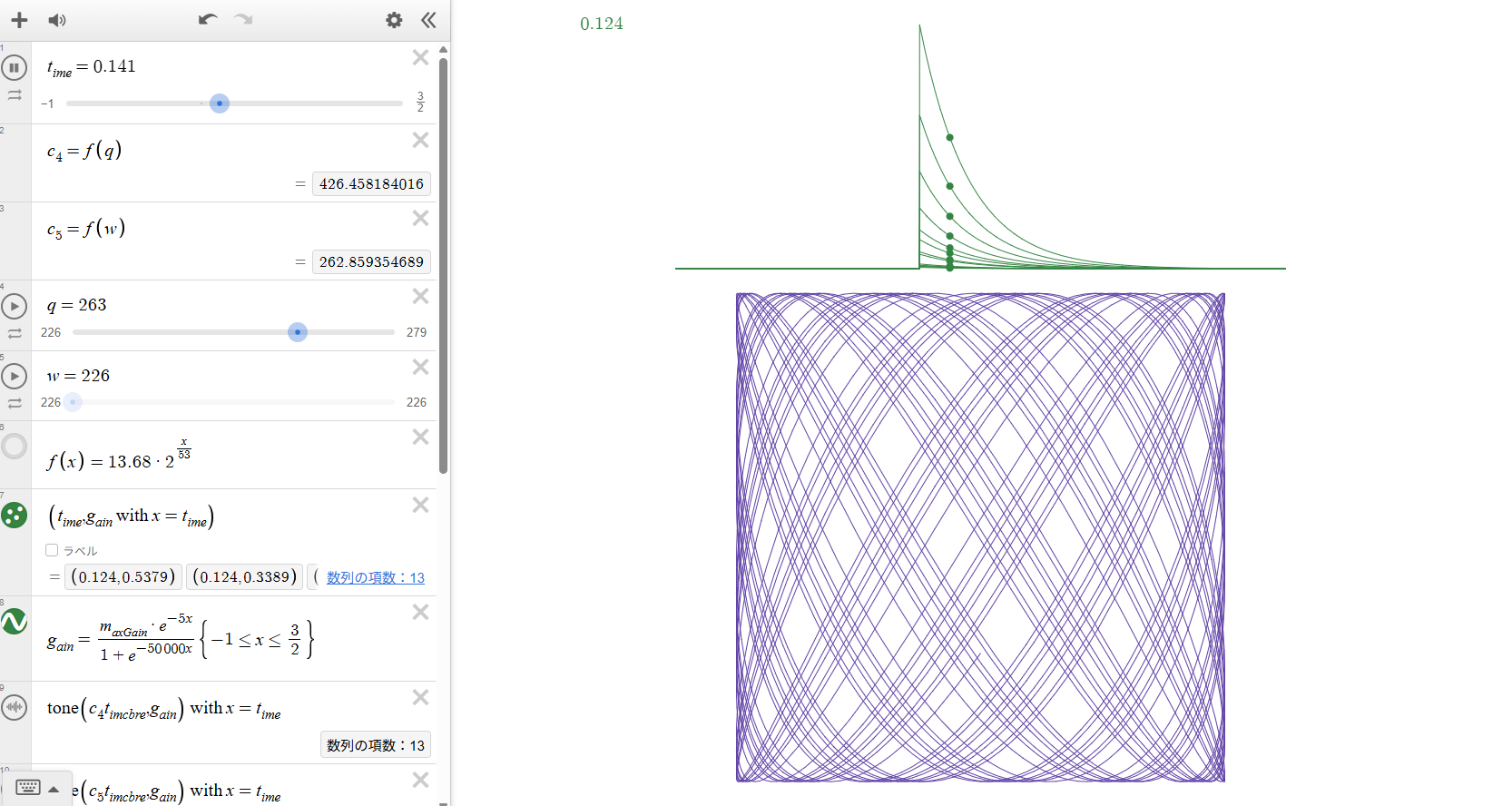
Sigmoid Decay and Harmonic Amplitude Distribution

Depiction of the sigmoid-based damping envelopes for each harmonic. The amplitude of 13 overtones is adjusted through the predefined gain array.

Desmos Parameter Configuration

Definition of key variables including the time parameter, frequency mapping function \( f(x)=13.68 \times 2^{x/53} \), and tone synthesis combining \( t_{imcbre} \) and \( g_{ain} \).

Lissajous Curve Transformation

Transition from a simple harmonic figure to dense periodic crossings as \( q \) increases, illustrating frequency interaction in 53-EDO.

Synchronized Sound–Shape Visualization

Simultaneous representation of the decaying waveform and corresponding Lissajous motion, visualizing the acoustic damping and harmonic convergence in real time.