IV as Dominant — An 11-limit 9-note Just Scale (V Tones Included, No V Triad)

Overview:
This scale starts from the idea of not using the V triad (G–B–D) at all as a chord, even though the tones that could form V are present in the pitch set. Instead, it asks: Can IV be made to function like a dominant?

The scale is a 9-note just-intonation scale (10 notes including the octave), built from the ratios:
1/1, 81/80, 5/4, 81/64, 4/3, 3/2, 5/3, 7/4, 63/33, 2/1.
Some of these tones are chosen so that they lie within the first eight partials of the harmonic series. The result is not a huge global tuning system, but a compact, performable scale designed for harmonic experimentation.

The scale is 11-limit because the tone at \(63/33\) contains the 11th partial in its internal structure.
Around the tonic, both \(1/1\)–\(5/4\) and \(81/80\)–\(81/64\) form pure major thirds of size \(5/4\). In 12-TET terms, these behave like two different “C–E” pairs coexisting inside one system.
These pairs differ by a syntonic comma; by switching between them, the performer can create changes in nuance. In addition, this design allows the intentional creation of vibrato-like beating inside harmonies.

Note: All content on this page is originally explained by Reiji in Japanese. The English version is translated by AI and structured by a parent, with Reiji's final approval.

Reiji's Words and Ideas

• Pitch set and why it is 11-limit
  This scale consists of the ratios
  1/1, 81/80, 5/4, 81/64, 4/3, 3/2, 5/3, 7/4, 63/33, 2/1.
  It is 11-limit because the final tone \(63/33\) has a structure that involves the 11th harmonic.
  Internally, it can be thought of as including an \(11/8\) relationship, so the third harmonic becomes \(33/32\).
  When a \(2/1\) is added and the value \(33/32\) is kept as it is, the 2/1 side is shifted from the 64th harmonic to the 63rd harmonic, and the span becomes \(63/33\).
  In this way the 11th partial is built into the structure, so the scale can be regarded as 11-limit.
  Also, by aligning some tones within the first eight partials of the harmonic series, the scale remains a compact just-intonation system in which the overtones are easy to imagine.
• Two “C–E” pairs: \(1/1\)–\(5/4\) and \(81/80\)–\(81/64\)
  The interval from \(1/1\) to \(5/4\) is a pure major third.
  Likewise, the interval from \(81/80\) to \(81/64\) is also a major third of size \(5/4\).
  In 12-TET terms, both pairs can function as a kind of C–E relationship.
  
  Therefore, within this scale, both \(\{1/1,\, 5/4,\, 3/2\}\) (a just major triad) and \(\{81/80,\, 81/64,\, 3/2\}\) can serve as “C–E–G”-type chords.
• The syntonic comma and perceptual tolerance
  If we reinterpret \(81/80\) and \(81/64\) as if they were \(1/1\) and \(5/4\), then the “fifth” above them is not \(3/2\) but \(40/27\), which is about 21 cents lower than \(3/2\) (one syntonic comma).
  
  In theory this changes the harmonic structure, but if we assume that the threshold for clearly hearing a pitch difference is around 5 cents, then 21 cents is about four times that threshold while still being musically usable as a difference in colour rather than simply a tuning error.
• Names of chords inside this scale
  Within this 9-note set, Reiji uses the following labels for chords:
  
  • \(1/1,\, 81/80,\, 3/2\) — a minor chord (m)
  • \(1/1,\, 5/4,\, 3/2\) — a Just Major chord (JM)
  • \(1/1,\, 81/64,\, 3/2\) — a Pythagorean Major chord (PM)
  • \(1/1,\, 4/3,\, 3/2\) — used as a sus4 chord
  • When the reference is \(5/3\), the original \(1/1\) becomes \(6/5\) and the original \(5/4\) becomes \(3/2\).
    The chord formed by these three tones is called 5/3m (5/3 minor chord).
• Example progression where IV functions as dominant
  One progression considered in this system is:
  1/1JM → 5/3m → 4/3JM → 1/1PM → 4/3JM → 1/1JM
  
  When mapped to 12-TET, this corresponds roughly to
  I → vi → IV → I → IV → I.
  Here, IV not only leads back to the original I, but also moves between JM and PM, playing a dominant-like role in relation to slightly different versions of the tonic.
• Intentional “vibrato-like” beating
  Within this scale there are specific combinations of tones that produce strong beating.
  For example, adding \(81/80\) to a 1/1JM chord introduces a slight detuning inside an otherwise almost perfectly just harmony, creating a vibrato-like effect.
  
  Similar effects appear with combinations such as 1/1JM and 81/64, 1/1PM and 81/80, and 1/1PM and 5/4.
  By inserting these “slightly off” relationships at chosen moments, the performer can build natural shimmer and motion directly into the chords.

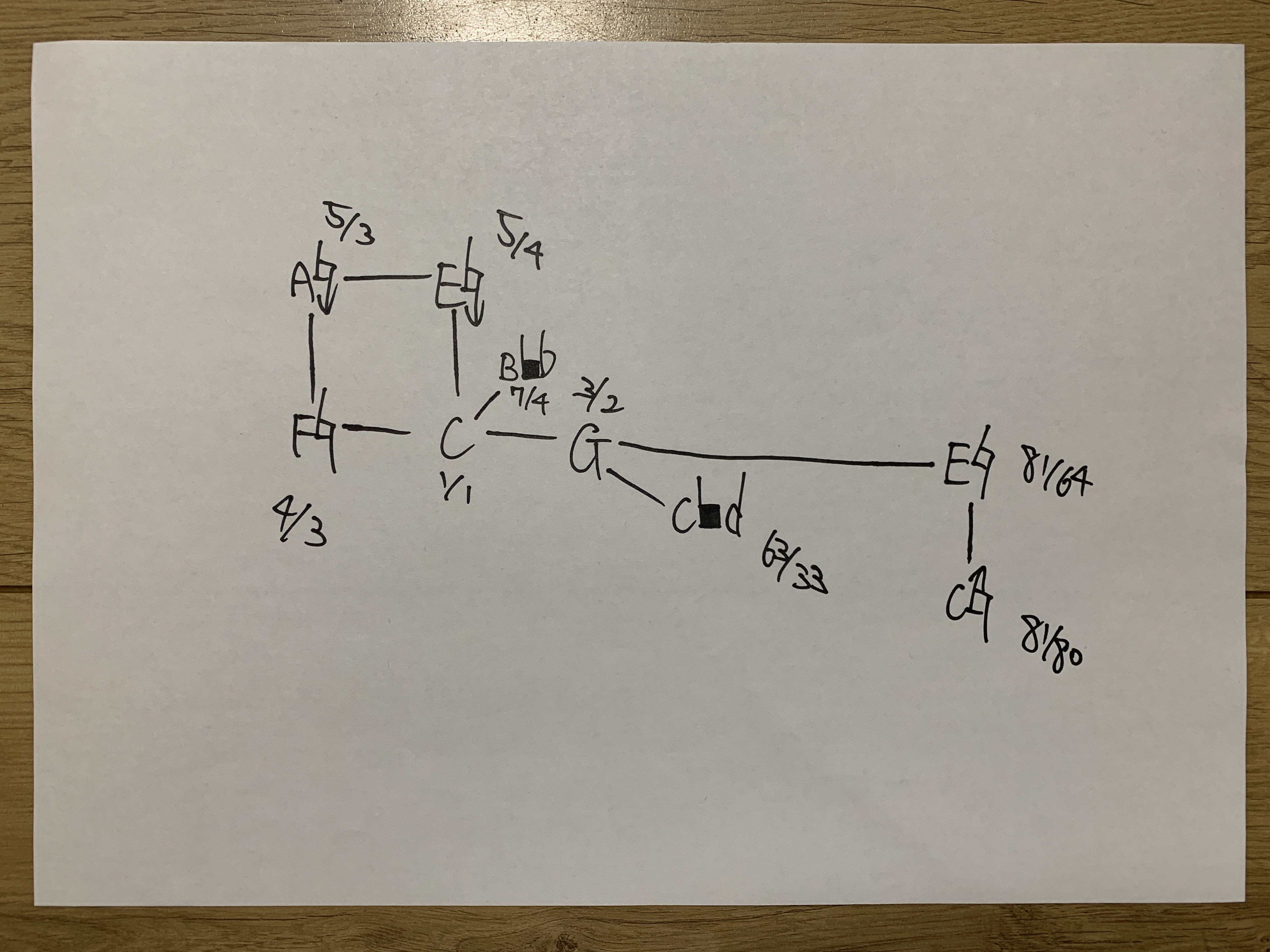
Hand-drawn Lattice of the 9-note Just Scale

A hand-drawn lattice diagram connecting tones with ratios such as 5/4, 4/3, 3/2, 7/4, and 63/33.
It organizes which tones are derived from which others, and by which ratios, using lines and fractional labels.

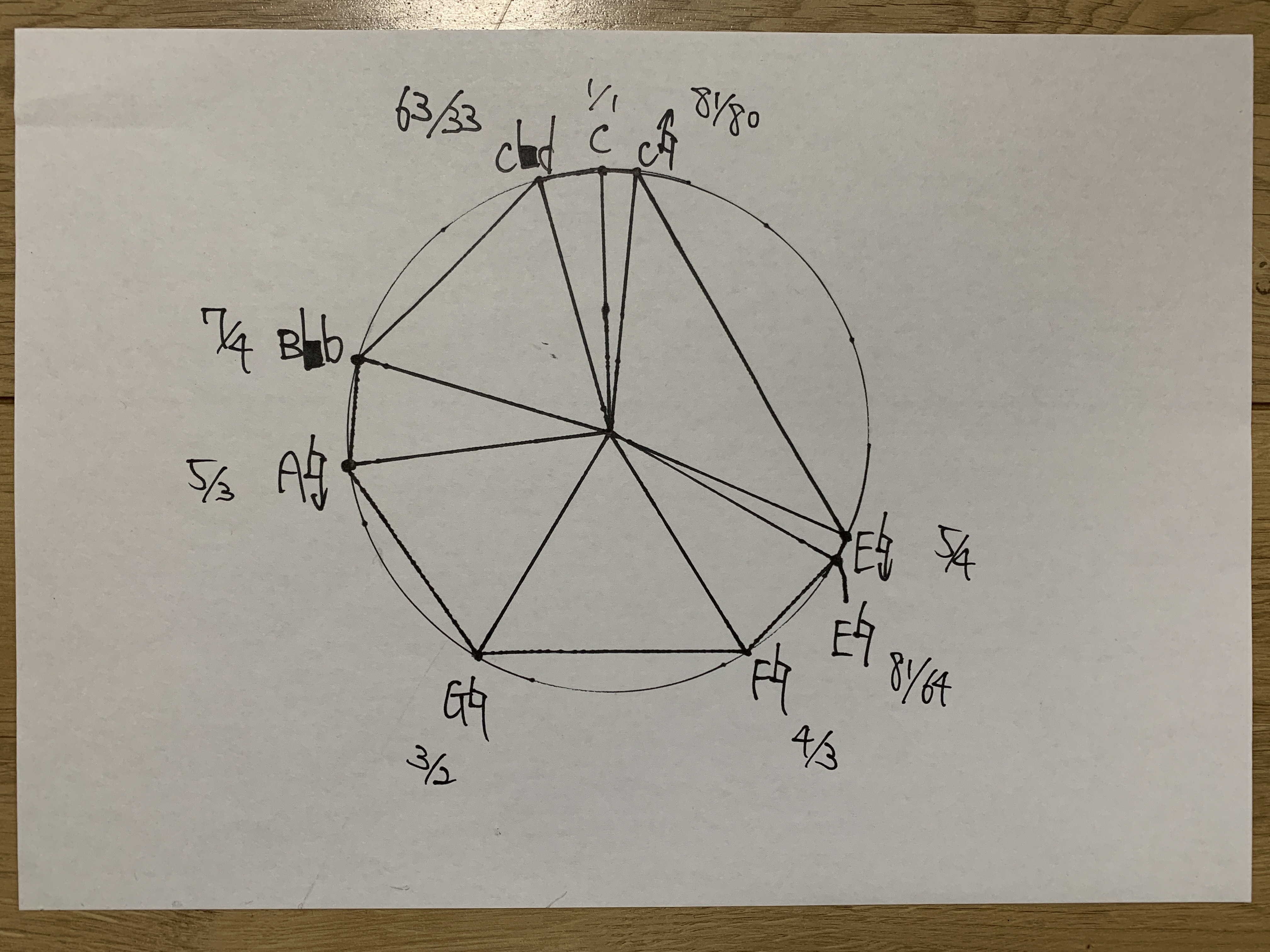
Radial (Circular) Diagram of the 9-note Scale

A hand-drawn diagram inspired by Entonal Studio’s “Graph” view, placing nine tones around a circle and drawing lines out from the centre.
Each point is annotated with a note label and its ratio (e.g., 5/3, 7/4, 63/33, 81/80), making the overall structure of the scale visible at a glance.

Stepwise Intervals When Tones Are Ordered from Low to High

A linear diagram in which all tones of the scale are placed in ascending order,
and the steps between them are labelled with ratios 81/80, 10/9, 81/80, 56/45, 9/8, 10/9, 21/20, 21/11, 66/63 …
It reveals the non-uniform spacing between neighbouring tones and the characteristic “uneven density” of this scale.

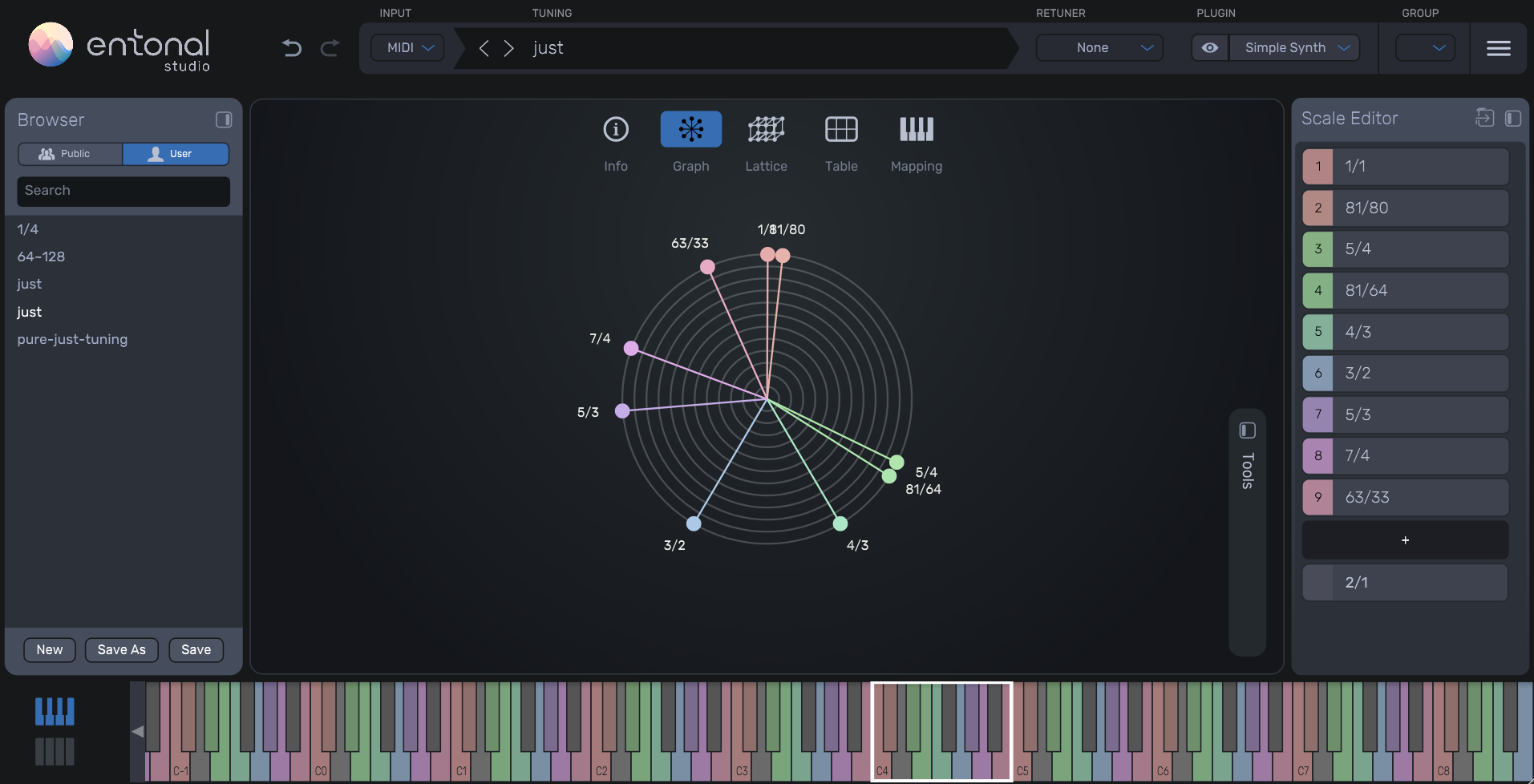
Graph View in Entonal Studio

Entonal Studio’s polar “Graph” view displaying the nine tones as vectors from the origin.
The distances show how far each ratio lies from 1/1 on a logarithmic scale, serving as a software-based verification of the hand-drawn radial sketch.

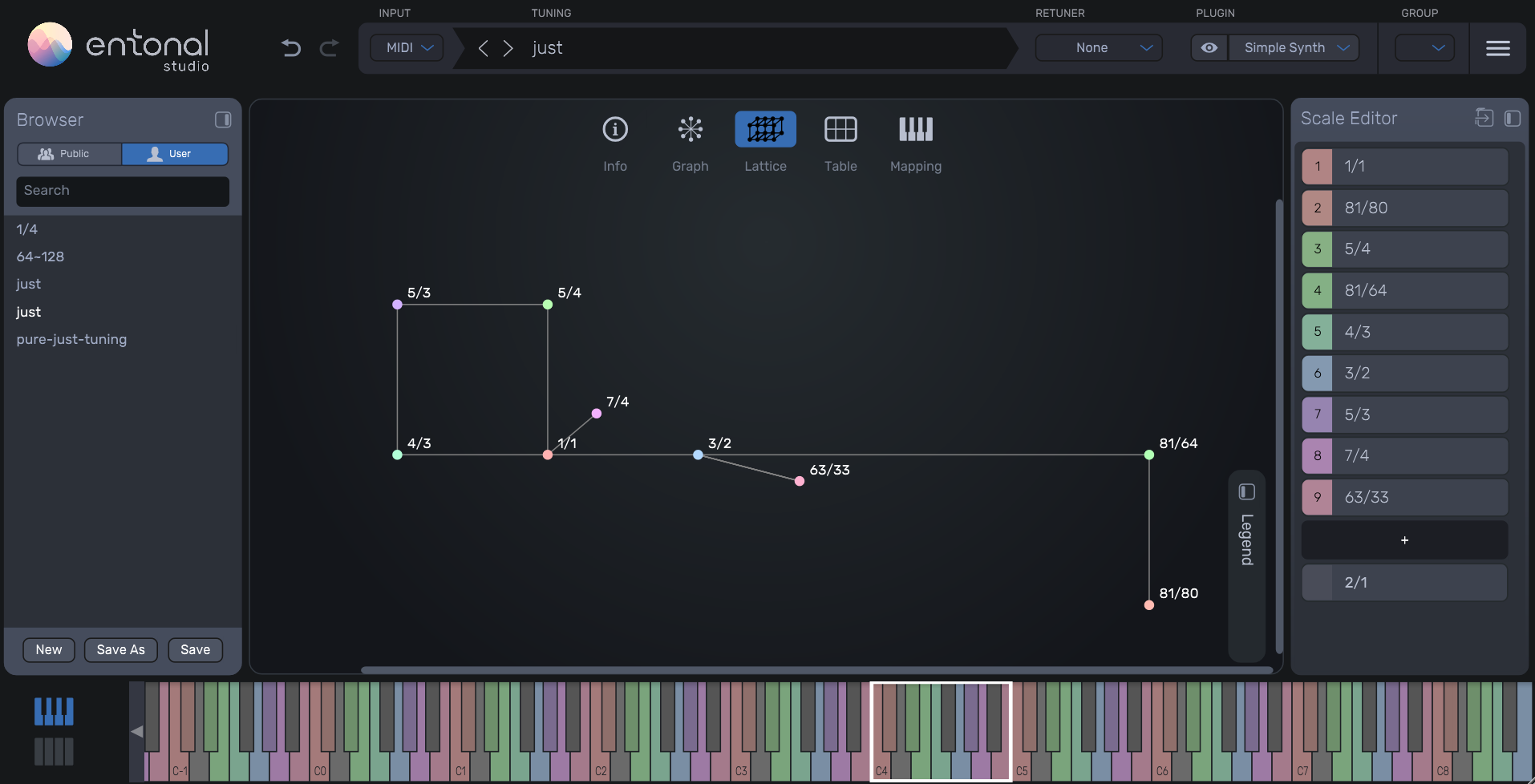
Lattice View in Entonal Studio

Entonal Studio’s “Lattice” view, in which 4/3, 5/3, 5/4, and 1/1 form a rectangle, and tones such as 3/2, 7/4, 63/33, 81/64, and 81/80 extend from it like branches.
It spatially arranges the relationships between just ratios (5/4, 4/3, 3/2, etc.), digitally reconstructing the structure of the hand-drawn lattice.

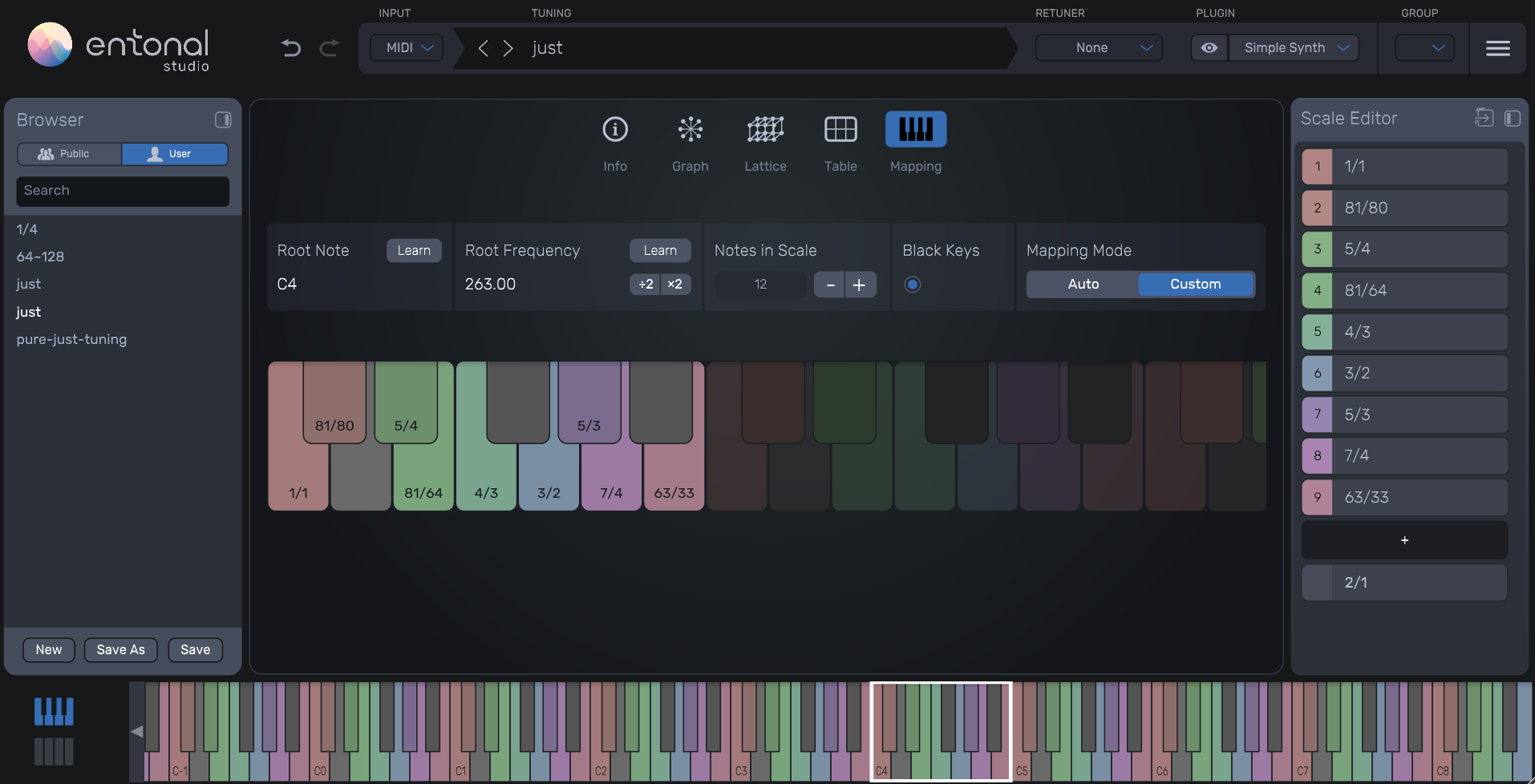
Keyboard Mapping in Entonal Studio

A mapping around C4 in which the ratios 1/1, 81/80, 5/4, 81/64, 4/3, 3/2, 5/3, 7/4, and 63/33 are assigned to individual keys.
This layout allows the performer to test progressions and voicings in which IV is treated as a dominant function, while directly hearing the differences between JM, PM, and slightly detuned variants.